练习课的导入方法及效果

练习课是课堂教学的重要组成部分，是在学生理解新知识的基础上，为巩固所学知识、形成技能的一种基本活动方式。它以学生的独立练习为主要内容，是培养学生能力的一种重要手段。一节成功的练习课离不开艺术性的导入，理想的导入会引起学生的浓厚兴趣，提高学习效果。数学练习课与新授课比较，未免显得平淡无味，那么该如何讲究导入呢？就此略谈以下几点练习课课堂常用的策略。

（一）揭示主题，明确要求

练习课是新授课的延续，以做练习为主，这样的课如果在导入阶段不能对学生明确要求，而只是让其盲目地做题练习，很容易使学生产生兴味索然的感觉。所以，有效的练习课应该先让学生明确练习课的目的和要求，而导入时直接揭示主题，明确要求是最有效的措施之一。

例如，在讲“圆锥的体积练习课”时，有一位老师是这样单刀直入，揭示主题导入的。

教师：同学们，今天这节课，我们要进行圆锥体积的练习。通过这节课的练习，第一要让我们进一步熟练掌握圆锥体积的计算方法；第二能运用已掌握的相关知识解决日常生活中的实际问题。今天我们要看一看，比一比，哪些同学积极动脑，踊跃发言，学得扎实，学得灵活和轻松！

教师在导入阶段用短短的几句话把这节课的目的、要求传播给了学生，这样可以使学生在后面的练习中目的明确，学习效率高。

（二）创设情境，趣味导入

在教学中要培养学生正确的数学应用观，对于抽象的数学知识，创设生动有趣的练习情境能吸引学生主动地高效率地参与学习，培养学生自觉应用数学的意识，能让学生真正掌握知识，使数学知识生活化，从而提高数学知识的应用能力。

例如，在执教“三角形的特性的练习课”中，一位教师是这样导入的。

教师：同学们，我们上节课学习了什么知识？

学生：三角形的特性。

教师：学习了这个知识后，昨天张涛组的同学在张涛爸爸的带领下来到了建筑工地进行参观，瞧！（多媒体出示建筑工地画面）他们在这儿遇到了不少这一单元中我们学习的知识，而且他们在这儿还帮工人叔叔解决了一些数学问题呢！大家想知道他们都遇到了哪些问题和他们是怎样解决的吗？

学生：（齐声，响亮地）想！

教师：好，这节课我们就跟随张涛组的同学们，一起走进建筑工地，看看我们能否也一起帮忙解决一些问题。（板书课题：三角形的特性的练习课）

在这样的环境中导入练习，学生必然兴趣盎然地投入学习，从中获得丰富的学习体验。他们体验到生活中存在着丰富的数学知识和数学问题，体验到数学知识的价值，体验到自己成为学习主人的乐趣。

（三）生成材料，铺路导入

“铺路”是指学生参与练习材料的生成和呈现，旨在把教材中静态的知识设计成动态的教学过程，为之后的练习过程展开铺好路，体现学生的学习主动性和对生成材料的负责性。

例如，某位老师在执教“三角形面积计算练习课”时，是这样在导入环节生成学习材料的。

（在大屏幕上出示图3-8）

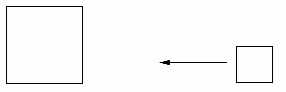
图3-8

教师：有两个大小不同的正方形，把小正方形向左平移，使两个正方形有一个顶点重合，你能想象一下得到了怎样的图形吗？

学生：两个正方形背靠背的样子。

教师：（课件演示小正方形平移的过程，变成图3-9）是这个样子吗？

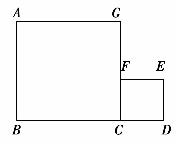
图3-9(www.xing528.com)

学生：是。如果继续平移下去，小正方形在大正方形里面，再继续平移，小正方形又要跑到大正方形外面了。

教师：说得好，现在我们就让它停止在这儿了。（标注顶点的字母）这是一个组合图形，它有几个顶点？

学生：（数一数）有7个。

教师：如果从7个顶点里选3个，用线段依次连接起来，可能得到什么图形？

学生：三角形。因为有3个顶点。

教师：你能根据图形的特征来思考很好，但是我选B、C、D三个点能得到三角形吗？看来只能选不在一条直线上的点。我先定一个点，另外两个点你们说了算。我选F点。

学生：我选B和C。

教师：可以得到什么三角形？

学生：直角三角形。

教师：像这样任意选三个顶点，可以画出许多三角形，你想试一试吗？（为之后求三个顶点围成的三角形面积埋下基础）

通过引导学生主动参与到理解问题情境的活动中，并独立画图生成进一步练习三角形面积所需要的材料，增强了学生对练习课的学习积极性。

（四）错题呈现，反馈导入

在练习课上，教师如果简单地让学生操练，学生的兴趣肯定不高。因此可以把平时的错例利用起来，以达知识的“实”。但为了吸引学生的学习兴趣，可以改变错例的呈现形式，导入练习课。

例如，在执教“两位数乘两位数的笔算练习课”时，一位教师是这样导入课堂的。

（教师直接课件呈现学生新授课后作业中的错误，如图3-10）

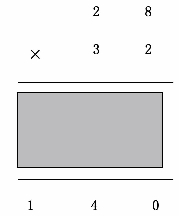
图3-10

教师：大家看，这是大家作业中的一道题，有位同学是这样做的。你觉得这道题算对了吗？

学生1：不对。

学生2：估算，30×30=900。

学生3：积的个位不是0。

教师：你猜猜看，它为什么错了？

学生4：数位对错了。

之后，打开遮住部分。

教师：第一层的56是怎么来的？（28×2）第二层看到的84怎么来的？（28×3）……

在这个导入中，教师改变了错例的呈现方式，如28×32竖式计算过程中被遮住了一部分，保持一种神秘感，这有利于激发学生的探究欲望，另外同时也回忆了两位数乘两位数笔算乘法的简单算理，为接下来的对新授课知识的补充和延续起了个好头。