“数学化”过程是指实现数学的再发现和再创造的教学过程,即从学生熟悉的现实生活开始,沿着人类数学发现活动的轨迹,从现实中的问题到数学问题,从具体问题到抽象概念,从特殊关系到一般规则,逐步让学生通过自己的发现去习得数学、获取新知,帮助学生把头脑中已有的那些非正规的数学知识和数学思维上升发展为科学的结论,实现数学的“再发现”。数学化是一种组织与构建的活动,它运用已有的知识与技能去发现未知的规律、关系和结构。虽然,学生要学的数学知识都是前人已经发现的,但对学生来说,仍是全新的、未知的,需要每个人再现类似的创造过程来形成。数学知识的学习并不是简单的接受,而以再创造的方式进行。数学教师的任务在于返璞归真,把数学的形式化逻辑链条恢复为当初数学家发明创新时的火热思考。
“活动过程”是指最终得到数学结论的数学活动过程。这里的“过程”包括两个方面:①发现实际问题中的数学成分,并对这些成分做符号化处理,把一个实际问题转化为数学问题,这是“横向数学化”过程;②在数学范畴之内对已经符号化了的问题做进一步抽象化处理,从符号一直到尝试建立和使用不同的数学模型,发展更为完善、合理的数学结构,这是“纵向数学化”过程。教师设计的教学活动要有利于体现活动过程,有利于学生进行真正的探究活动,让学生在活动过程中理解一个数学问题是怎样提出来的、一个数学概念是怎么形成的、一个数学定论是怎样获得和应用的,让学生在活动过程中学习和应用数学。
例如,人教版一年级上册认识加法意义的数学情境(如图2-1)。在这个数学情境中,蕴含的数学问题是“3和1合起来是多少”,教师引导学生参与活动过程进行操作、思考。
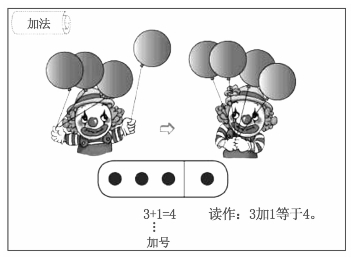
图2-1 加法教学图
(1)数数小丑先生一只手拿着几个气球,就请画几个圆圈。
(2)数一数小丑先生另一只手拿着几个气球,继续画几个圆圈。于是,每位学生都会画出下面的图形:○○○○。
(3)数一数你一共画了几个圆圈。(https://www.xing528.com)
(4)与同桌说一说你所画的这几个圆圈表示什么意思。
事实上,这样的数学活动过程就是学生在操作、思考水平上解决加法问题的过程,尽管他们还没有规范叙述什么是加法。在解决问题的过程中,学生慢慢在心理上构建着加法的数学结构,即3个与1个气球合在一起是4个气球。在此基础上,引入正规的数学符号表示:3+1=4。这就是学生亲身经历将实际问题抽象成数学模型(加法结构),体会加法的意义的过程。
又如,人教版小学数学教材二年级上册,认识乘法的数学情境(如图2-2)。相同加数的连加算式表示为5+5+5=15。问题是如果相同加数的个数越多,连加算式的表达和计算越麻烦。引进数学中的乘法,就是为了解决这个“麻烦”。也就是为了简缩相同加数的连加算式,从而体现乘法诞生的必要性,用如下乘法表示:3×5=15或5×3=15。这两个乘法算式都表示3个5相加的意义,都是对上述两个连加算式的抽象与概括。换言之,乘法算式是重新塑造相同加数连加算式的思维。
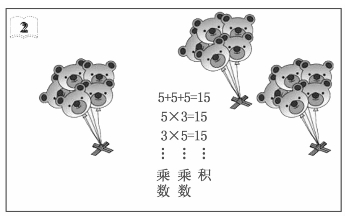
图2-2 乘数教学图
当然,从整个学习过程来看,学生无法自己创造出乘法。教师必须让学生体验产生乘法的必要性,体会乘法与加法的本质的联系。
上面的第1个例子体现的是“横向数学化”过程,第2个例子体现的是“纵向数学化”思想。“活动过程”强调学生学习活动的探究性、过程性。教师设计的教与学活动中要让学生进行真正的探究,并在思维过程的历程中实现数学化和再创造的过程。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




