县第二产业增加值存在空间滞后效应，负效应转正

在做固定效应的空间面板回归之前，先做没有空间效应的回归，作为参照，其Stata语句是：

. xtreg y x1 x2 i.year， fe

回归得到的组内R2值是0.0641，组间R2值是0.2837，总体R2值是0.1489。F值是70.1，Prob ＞F=0.0000。回归得到的sigma_u值是75177.41，sigma_e值是89857.892，而rho值0.412。

表6-15：固定效应面板模型结果

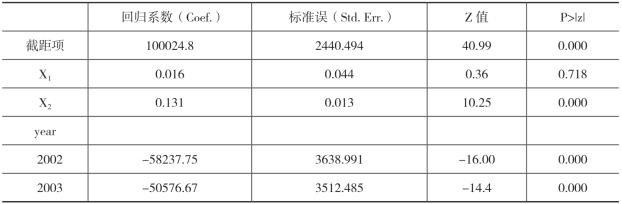
比较表6-1和表6-15，发现通过固定模型进行回归，X1的回归系数从显著变成了不显著。X2的回归系数尽管依然是显著的，但是，其值明显变小了。此外，年份虚拟变量回归系数的绝对值也明显变小了。

把空间滞后因变量引入到模型中，成为其中的一个自变量，在采用邻近空间权重矩阵进行固定效应空间面板模型回归，其Stata语句是：

. spxtregress y x1 x2 i.year， fe dvarlag（Wp）

得到的结果如下：Wald chi2（5）值是280.67，Prob ＞chi2 =0.0000，“准R2”（Pseudo R2）值是0.1489。对数似然函数（Log likehood）值是-52320。对于这个空间误差项的Wald检验，其chi2（1）值为0，Prob ＞chi2 =0.9763。回归得到的sigma_e值是89813.99。

表6-16：固定效应空间面板模型结果（空间滞后因变量）(www.xing528.com)

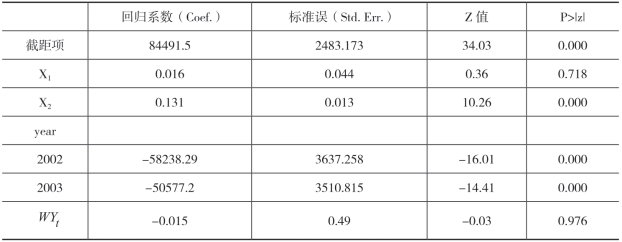
加入空间滞后因变量滞后，固定效应空间面板模型的回归结果显示，因变量空间滞后效应并不显著。不过，也不能简单就此得出结果，认为因变量空间滞后效应必定不存在。

若在空间面板回归模型中，改变空间权重矩阵，用反距离权重空间矩阵替换邻近空间权重矩阵，其Stata语句是：

. spxtregress y x1 x2 i.year， fe dvarlag（Mp）

得到的结果如下：Wald chi2（5）值是1477. 33，Prob ＞chi2 =0.0000， “准R2”（Pseudo R2）值是0.003。对数似然函数（Log likehood）值是-52370。对于这个空间误差项的Wald检验，其chi2（1）值为1171.88，Prob ＞chi2 =0.0000。回归得到的sigma_u值是42058.46，sigma_e值是86093.51。

表6-17：固定效应空间面板模型结果（空间滞后因变量与反距离权重）

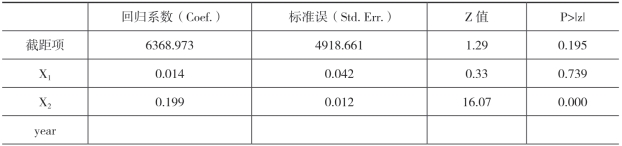
续表

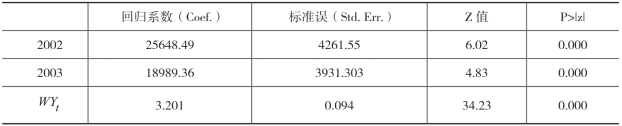
比较表6-16和表6-17， X1的回归系数依然是不显著的，而X2的回归系数同样是显著的。这说明，空间权重矩阵的变化，对这两个自变量的显著性都没有影响。在比较年份虚拟变量，发现了明显的不同，这些虚拟变量的回归系数都还是显著的，但是，其系数都已经从负数变成了正数。可见，空间权重矩阵的变化，对于这些变量而言，产生了明显的影响。此外，从WYt的回归系数来看，也有变化。之前是不显著，显著变成了一定程度上的显著。这些变化都表明，空间权重矩阵的调整，往往会产生一定的影响和作用，因此，在研究过程中，要谨慎分析不同空间权重矩阵的影响，避免出现以偏概全的错误出现。