经济学中的产业发展与统计方法

在经济学中，产业发展是一个重要的研究领域。比如要研究第二产业发展的情况，用第二产业增加值作为因变量，探讨从业人员和固定资产投资对于第二产业发展的影响。那么，方程式就是：

其中，Y是因变量，这里是指第二产业增加值（万元）；X1是一个自变量，是指年末单位从业人员数（人）；X2是另一个自变量，是指城镇固定资产投资完成额（万元）。数据来自《中国县域统计年鉴 2002》，剔除了有缺失值的县，研究样本共有2048个县。

在进行空间回归之前，先进行Moran’s I检验（Moran’s I test）。Moran’s I检验检验是用来测量和检验在总体上空间自相关性的重要统计方法，因此，又被称为全局性的空间自相关检验（Moran’s I检验）。也就是说，Moran’s I检验是从总体上来检验样本空间观测点上的数据彼此相似的程度，从而来判断整体上样本数据是否具有空间自相关性。在实际操作中，就是计算Moran’s I值并检验其显著性。Moran’s I值的计算公式如下：

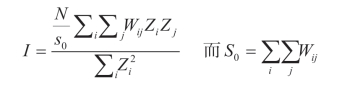
其中，Zi是目标变量对于其均值的偏差；Wij是空间权重矩阵。

可见，要进行Moran检验，就需要有给定空间权重矩阵。若没有给定空间权重矩阵，就无法计算Moran’s I值，也就无法进行Moran’s I检验。在本例中，计算了两种类型的空间权重矩阵，分别是邻近空间权重矩阵和反距离空间权重矩阵。在Stata中的语句是：

. spmatrix create contiguity W

. spmatrix create idistance M

这里的W就是邻近空间权重矩阵，而M 就是反距离空间权重矩阵。

在进行Moran检验前，首先可以进行没有空间因素的回归分析，其回归方程式是：

在Stata中的语句是：

. regress Y X1 X2

通过回归得到的结果是：

表5-1：OLS回归结果

根据表5-1的结果，两个自变量的回归系数都是正数，而且都是显著的。但是，这个回归结果是否可靠，还需要对这个回归后的残差进行进一步的检验，就是Moran’s I检验。这里，分别通过邻近空间权重矩阵和反距离空间权重矩阵对回归得到的残差计算Moran’s I值，并进行统计检验。在Stata中的语句分别是：(www.xing528.com)

. estat moran， errorlag（W）

. estat moran， errorlag（M）

Moran’s I检验的结果如下：

表5-2：Moran’s I检验结果

根据表5-2所示，Moran’s I检验的结果显示，当此用邻近空间权重矩阵时，Moran’s I检验并不显著，这说明在这种空间权重矩阵下，目标变量并不存在空间自相关性，因此，没有必要通过空间回归模型进行回归，即现有的回归模型已经足够了。但是，当空间权重矩阵发生了变化，那么，这个结论就不一定成立。当采用了反距离空间权重矩阵时，Moran’s I检验显著，这说明在这种情况下，存在着显著的空间自相关性，因此，需要通过空间回归模型进行回归和估计。所以，本例子主要采用的是反距离空间权重矩阵进行各项空间回归，但是，为了比较，同时也会采用邻近空间权重矩阵进行空间回归。

在空间回归估计中，采用广义空间二阶最小二乘（Generalized Spatial Two Stage Least Square，简称GSTSLS）方法。对于空间权重矩W，这里采用了反距离权重（Inverse DistanceWeighted，简称IDW）。这种方法定义不同距离之间的邻近关系时遵循了“地理学第一定理”：研究对象距离越远，它们之间的相互影响越小。

回归后，出来结果。Wald chi2（3）值是399.87，Prob ＞chi2 =0.0000，“准R2”（Pseudo R2）值是0.1079。

表5-3：空间滞后模型结果（广义空间二阶最小二乘法）

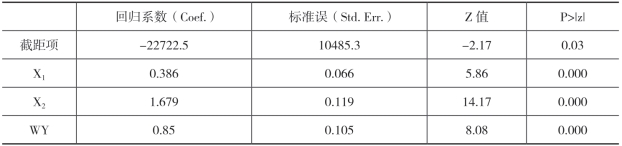
根据表5-3所示，两个自变量年末单位从业人员数和城镇固定资产投资完成额对于第二产业增加值的影响都是正向且显著的。这说明，随着年末单位从业人员数和城镇固定资产投资完成额的增加，第二产业增加值也会随着增加。也就是说，工业产值的增加与劳动力和资本投入有关。对于一个工业系统而言，劳动力和资本都是其发展的基本生产要素。随着劳动力和资本投入的增加，在既定的技术条件下，工业产值也会随着增加。

此外，邻近县之间的工业发展情况也会互相影响。表5-3所示，模型估计的空间自回归系数是0.85，且是统计显著的。对于这个空间项的Wald检验，其chi2（1）值为65.36，Prob ＞chi2 =0.0000，这说明这个空间滞后因变量对于因变量自身的影响是显著的。也就是说，邻近县之间在发展工业上是彼此依赖的，存在着显著的空间自相关性。这说明在工业发展上，邻近县之间往往会存在着正向的溢出效应（Spillover Effect），即一个县工业的发展，往往会带动周围邻近县工业的发展。造成这种现象的原因是多方面的，比如相邻县之间的彼此学习效应、邻近县之间工业系统的互补性和专业分工，等等。

当然，还可以采用最大似然估计（Maximum Likelihood Estimation，简称MLE）方法进行空间滞后模型的估计。回归后，出来结果。Wald chi2（3）值是545.13，Prob ＞chi2 =0.0000，“准R2”（Pseudo R2）值是0.1516。对数似然函数（Log likehood）值是-27375.668。对于这个空间项的Wald检验，其chi2（1）值为210.07，Prob ＞chi2 =0.0000。

表5-4：空间滞后模型结果（最大似然法）

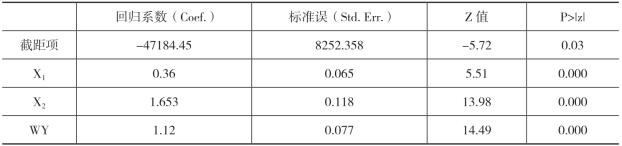
比较表5-3和表5-4，发现通过广义空间二阶最小二乘法和最大似然估计法进行空间滞后模型的回归估计，两个常规自变量X1和X2对因变量的影响，无论从估计系数大小还是其显著程度上，都基本上相似。但是，空间自回归系数的估计值却从0.85增加到了1.12。也就是说，在这个例子中，在最大似然估计法中，邻近县之间在工业发展上的彼此依赖性会更强。这是估计方法对于系数的影响。不同的估计方法，对于空间自相关性程度的估计有所不同。在本例子中，最大似然估计法比广义空间二阶最小二乘法所得到的系数要更大。

在实证研究中，广义空间二阶最小二乘法和最大似然法都有其使用的前提假设。广义空间二阶最小二乘法的前提假设是残差是独立同分布的，但是，可以不是正态分布。在空间回归上，这种方法适用性比较广。最大似然法除了要求残差是独立同分布之外，还要求符合正态分布。可见，最大似然法的前提条件要比广义空间二阶最小二乘法更高。相对而言，最大似然法应用范围也就比较窄。在空间回归模型中，一般只能用于一个空间滞后因变量和一个空间误差项，但是，可以用来估计多个协变量空间滞后（multiple spatial lags of covariates）的模型。在实际回归过程中，有时候也需要在不满足正态分布的情况下，用最大似然法进行估计与回归。这属于强制进行最大似然估计的方法，在有些情况下，也是可以采用的。