主成分分析法：信息服务协同组织

在多元统计分析方法中，主成分分析法（Principal Component Analysis）是比较重要的一种^[12]。主成分分析将研究对象的多个相关变量（指标），通过坐标旋转进行降维，从而形成相互独立的主成分指标，然后通过相应的分析和权重计算，得到评价结果^[13]。

主成分分析基本算法的步骤如下：

①采集p维随机向量x=（x1，x2，…，xp）T的n个样本xi=（xi1，xi2，…，xip）T，i=1，2，…，n，n＞p，构造样本阵，对样本阵元进行如下标准化变换：

其中得到标准化矩阵Z。

②对标准化矩阵Z求相关系数矩阵：

③解样本相关矩阵R的特征方程|R-λIp|=0得到p个特征根，确定主成分：

按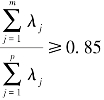确定m值，使信息的利用率达到85%以上，对每个λj，j=1，2，…，m，解方程组Rb=λjb，得到单位特征向量。(www.xing528.com)

④将标准化后的指标变量转换为主成分：

U1称为第一主成分，U2称为第二主成分，Up称为第p主成分。

⑤对m个主成分进行综合评价：

将m个主成分进行加权求和即得到最终评价值，权数为主成分的方差贡献率^[14]。

主成分分析法的应用也有一定的限制，因为并不是所有高维的数据都适合主成分分析。首先，在数学上，要求随机变量x1，x2，…，xp的协方差矩阵为p阶非负定矩阵；其次，指标数据需具有一定水平的相关性才适合做主成分分析；最后，主成分分析中因子负荷符号交替使得函数意义不明确，需要大量的统计数据，没有反映客观发展水平。