结论是我们用数据和证据对事实做出的最后的判断或决定。
我们根据事实推断,变量组4b中的根腐烂了。我们还根据事实推断,对照组B中的根没有腐烂。我们用两个推断和其他事实——如植物所处的变量——联系起来,就能得出结论。我们的结论是:变量组4b中植物所处的条件造成了根的腐烂。
虚假相关(spurious correlations):虽然有些有趣的数据表明变量间的相关性,但我们无法认定变量间的因果联系。相关性(correlation)并不代表因果性,即便变量A与变量B的变化趋势一致,并不意味着是变量A的变化引起了变量B变化。
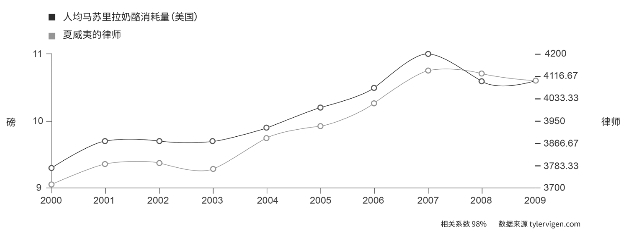
图10.4 美国人均马苏里拉奶酪消费与夏威夷的律师数量相关
虽然推测美国马苏里拉奶酪的消耗量对夏威夷的律师数量会产生怎样的影响很有意思,但是这两者之间并不存在因果关系。
负相关(inverse correlations)指的是随着自变量值的增大,因变量值反而会减小。
有时,变量间的相关关系“说得通”是因为两个变量间存在紧密联系。在下面的图中,随着马萨诸塞州的降水量的减少,由于割草机使用不当而致死的人数就上升。天不下雨人们就更可能使用(误用)割草机。然而,并不只有马萨诸塞州存在误用割草机致死的人。马萨诸塞州的天气不会影响加利福尼亚州使用割草机的人数。(https://www.xing528.com)
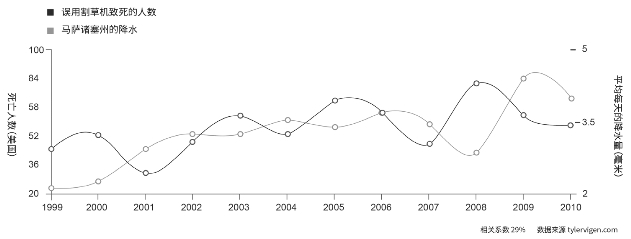
图10.5 误用割草机致死的人数与马萨诸塞州降水量呈负相关
虽然相关性不等于因果性,有些相关的变量间确实存在因果关系。如图10.6所示,在美国日本轿车的销量与美国进口原油总量有关。汽车销量的增减可能影响美国原油的进口量。使用的车越多,对石油的需求就越高。因为石油产业和汽车生产是有经济关系的,这两个变量间有密切联系。
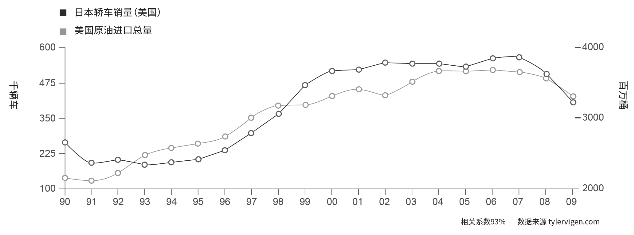
图10.6 美国境内日本轿车的销量与美国原油进口总量相关
然而,正如下图显示,美国的新车销售总量与美国原油进口总量无关。如果我们只看日本轿车在美国的销售数据,我们可能就得出了错误的结论。
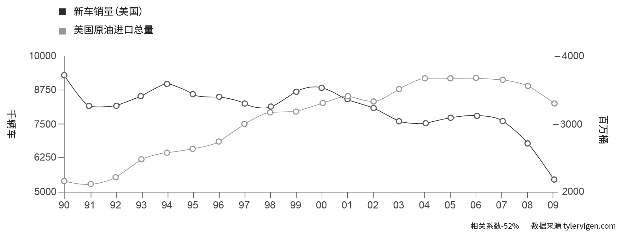
图10.7 美国新车销售数量与美国原油进口总量无关
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




