钟形曲线及其应用-科学研究原理

钟形曲线就是直方图表现出来的形状，在科学研究中经常出现。从成年人的身高到灯泡的寿命的统计制图都常常运用这种曲线或者它的变形。

图6.21显示了钟形曲线的基本形式。虽然两个图构成曲线的集合单元宽度不同，但是如果你把那些集合顶部连接起来，你会得到同样的形状。

钟形曲线的方程也称“正态分布”（normal distribution）：

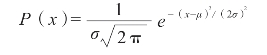
［这里P（x）是x的概率，μ是数据集的均值，σ是标准偏差，我们会在下面讨论］。

然而，与托里拆利定律的方程一样，你不需要通过解方程来绘制曲线。如果你的数据集是标准正态分布，你所需要知道的是均值（曲线的中心）和标准偏差。上面显示的曲线围绕着0，标准差为1。标准偏差较小的钟形曲线是又高又窄的，标准偏差较大的钟形曲线是又矮又宽的。

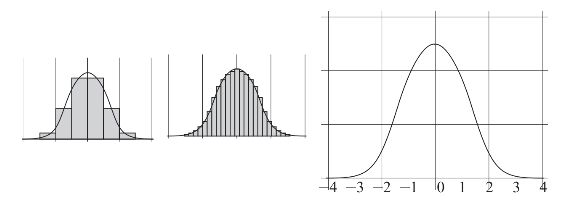
图6.21　钟形曲线

标准偏差(www.xing528.com)

数据集的标准偏差用于衡量在数据集中，各点（研究的变量的每次测量值）与所有点的均值的差别（偏差）程度。为了弄清楚这一点，科学家把所有的差别加起来，再除以数据集中的点的数量。数据集标准偏差的方程是：

在这里σ是标准偏差，N是在数据集中数据点的数量，μ是数据集的均值，表示从1到N的所有数据点进行后面的运算，然后把结果相加。一旦你知道数据集的标准偏差，你马上也知道了关于你的数据集的下列信息：

大约68%的数据点落在均值的一个标准偏差范围内；

大约95%的数据点落在均值的两个标准偏差范围内；

大约99.7%的数据点落在均值的三个标准偏差范围内。

钟形曲线，也叫做正态分布，是用于统计分析的几种概率分布（probability distributions）之一。它们之所以被称为概率分布，是因为它们表示x落在一个特定的集合单元或值的范围的概率。那个概率是该范围内的曲线面积。

有些分布，如伯努利分布（bernoulli distribution）与泊松分布（poisson distribution），是用发现它们的数学家命名的。而钟形曲线名字不是以贝尔博士命名的，而是因为曲线形状看上去像钟。