到目前为止,我们所讨论的数据集,其图表数据点都比较容易用一条直线或一条曲线表现。然而,有时数据集有很大的变化或随机误差,或者自变量变化率不一致,或者数据集不表示单射(即一对一)函数,或者甚至根本不是函数方程。在这些情况下,我们需要使用线性回归(linear regression)帮助我们从复杂的数据集中得到相应的数据图。
在本章开始的渗漏水管研究中,我们用平滑的直线帮助我们理解水管流量。但是我们也发现,在进行更为精确的测量时,流量会改变。我们可以提出一个假设:渗漏水管的流量取决于是否有坐便器刚刚冲水。为了测试这个假设,我们得找到流量和坐便器冲洗之间的关系。
我们怎么设计一个实验来发现流量和坐便器冲洗之间的关系呢?首先,我们得测量不同时间的流量,看它是否改变。为了计算简便,我们每隔一小时测一次。即我们每隔一小时测一次水桶里水的体积,就像先前研究中的那样,但是,我们不是要弄清楚整个实验期间的流量变化,而是不同小时内的流量变化。这很容易实现,我们只要看桶里水的体积变化就可以知道。例如,如果一小时内体积增加0.5升,该小时的流量就是0.5升/小时。
为了弄清楚坐便器冲洗的问题,我们可以让屋里的住户写下他们每次冲洗坐便器的时间。这样我们将得到第二个数据集,根据屋里所有坐便器的冲洗时间,我们可以从中弄清楚,每小时内坐便器被冲洗了几次。
为了了解一天的数据,让我们把实验延伸到过去的24小时。我们得把水桶倒空几次,或使用更大的水桶,但是因为我们在观察体积变化,而不单纯是体积,所以不会影响实验结果。首先我们选择在午夜测量。实验中,我们要记住的不是初始条件,而是基本流量:即近期没有冲洗坐便器得到的流量。收集的数据记录在表6.8中。
表6.8 渗漏水管实验数据

每小时冲洗次数和每小时流量之间的关系图表不是一般函数。有时每小时的冲洗次数与超过一小时时间段内的冲洗次数是相同的,有时,每小时的流量与超过一小时时间段内的流量也都是相同的。然而,因为测量时间对应的值不重复,即使“每小时冲洗”和“每小时流量”的值有一定重复,我们可以把“我们测量的时间”的值与另两个值关联起来,每个小时产生1个数据点,x是坐便器冲洗次数,y是流量(见图6.17):
对于这个数据集,正如我们上面注意到的,在x轴上的一些值(即每小时坐便器冲洗次数)在y轴上对应多个值(即每小时流量),而y轴上的一些值(即每小时流量)也在x轴上对应多个值(即每小时冲洗次数)。数据点看上去不是一条直线,而是离散的。事实上,这种图表叫做散点图(scatter plot)。
我们如何找出最能拟合这个散点图的直线?为了实现最佳拟合,我们找出一条最接近所有散点的直线,这个方法叫做线性回归,选择拟合直线的过程叫做曲线拟合(取决于数据分布,结果可能是一条曲线,但是在这个例子中,我们选择的是直线)。

图6.17 每小时流量-坐便器冲洗次数散点图
我们怎么评价拟合线和散点集的接近程度?一个简单的办法叫做最小二乘法(least squares method)。(https://www.xing528.com)
在图6.18中,直线代表的是函数y=(-0.07)x+0.5。
箭头表示数据集中的每个点到这条线的距离。
在数学上,我们可以通过比较直线的方程和数据集中的各散点找出这些点到线的距离。为了使距离为正(因为有些点在线下,有些在线上),我们要把距离平方。
表6.9列举了图上每个点的x值、y值、直线的方程算出的每个x值对应的y值、x值对应的实际y值、计算y值与实际y值之间的差,以及y值的差的平方。
这条线y值的差的平方的和是0.082。要通过人工计算弄清楚这根线是否是拟合度最高的拟合线,我们还需要核对一些其他线、斜率、截距和插值。所以,还有一种利用标准偏差(standard deviations)和偏导数(partial derivatives)进行运算找出最佳拟合线的办法。
大多数统计类计算机程序提供这样的函数运算。把数据集输入这些程序后,实验者所要做的就是选择目标拟合曲线(上述例子中选择的是直线,对于其他数据集,可能是抛物线或正弦波,或更复杂的情况)。
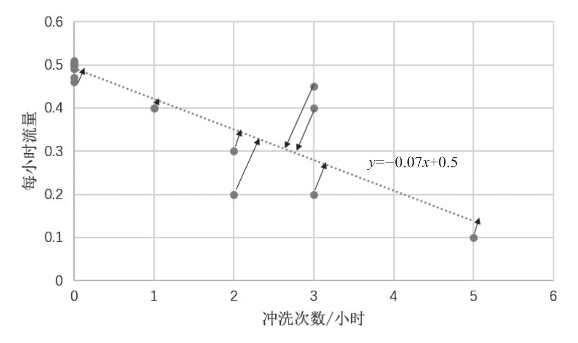
图6.18 曲线拟合例子
统计程序还会算出这根线的R2值,R2代表相关指数。R2值衡量线性回归线和数据点的拟合度。R2值为0意味着没有相关性。R2值为1意味着完全相关,即所有箭头的长度(为残差,residual)都是0。这张图的R2值是0.74。R2值是0.74意味着什么?意味着可能还有一条更适合这些数据点的线。然而,它还可能意味着会有其他因素影响漏水的流量,而这些因素没有被这个实验考虑进去(例如,测流量时有住户在淋浴,或者在给鱼缸换水)。如果实验的基本量有较大变化,这表明还有其他因素在影响因变量。
表6.9 最小二乘法计算结果统计表

(续表)

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




