科学研究原理：托里拆利定律及其应用

在上面水管和水桶的研究中，很幸运，我们的函数是条直线。但是，如果我们研究漏水率的对象是一个水箱而非是水管，研究结果会怎么样呢？

容器（例如水管、水箱甚至动脉或静脉）的渗漏率，取决于容器的压力以及漏孔的尺寸和形状。在我们的水管案例中，我们假设水管的漏孔大小和水管的压力都是不变的。

但是在像水箱这样的敞口容器中，容器内的压力取决于测量点的深度：测量点的水位（或任何液体）越深，测量点的压力越大（那就是为何当你游到泳池底部，你的耳朵感觉到有压力）。这种情况会怎样影响流量？

流量和敞口容器水位深度关系的数学公式被称作托里拆利定律（Torricelli’s Law），表达式是v=φ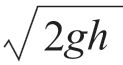。在这里，v表示流量，φ是代表三个其他常数（描述液体密度、漏孔尺寸和形状）的常数，g表示重力，h表示测量点上方液体的深度（或者高度）。［这个定律是以17世纪意大利物理学家和数学家埃万杰利斯塔·托里拆利（Evangelista Torricelli）的名字命名的，他发明了气压计］

托里拆利定律的函数图像是平方根函数的形状，v是y轴，h是x轴。函数图可以根据g（重力）和φ缩放，但是我们不知道φ是什么。

通过检查漏孔和测量液体密度算出φ是非常困难的，但是因为即使流量会变化，φ的值并不随深度改变而变化，并不需要检查漏孔或测量液体密度。工程师所要做的就是在某一时刻测量出洞口的流量，同时测出洞口上方的水深。然后，工程师可以把那些数字代入托里拆利定律的方程，算出φ的粗略值（当然，如果工程师想更准确，随着水位的下降，可在不同时间点测量几组流量和深度的数值，并把结果取平均值，算出φ）。一旦工程师算出φ，就能预测任何深度时的流量。从流量范围（只要水箱里的水不结冰），工程师就能算出在任何时刻漏出的水的体积。

托里拆利定律很难解释，但是容易演示，只需要一个空塑料瓶和一些水。(www.xing528.com)

在这个实验里，我们将用到几个不同高度的漏孔，而不是随着容器里水位下降的一个漏孔。但是，我们还是应该注意随着水位下降，底部漏孔的流量变化。

1.准备一个空塑料瓶和一些水，以及准备盛放漏水的容器。

2.在瓶上扎三个小孔，一个在底部，一个在中间附近，还有一个在瓶颈下。尽量使孔的尺寸和形状相同。

3.让人用手指堵住瓶孔，然后朝瓶里灌满水。

4.让瓶子保持直立，移开手指，露出瓶孔。