科研原理揭秘！比例与平移能帮助匹配数据

对于上面讨论的两张基于小时变化的渗透研究图，一张图中的因变量是“桶内体积”，另一张是“桶内剩余空间”，两张图中自变量和因变量的关系都可以用直线方程表示，也就是y=ax+b。对于“水桶水量升/小时图”，方程是y=0.5x+0，对于“水桶剩余空间/小时图”，方程是y=（-0.5）x+5。

如果我们把自变量和因变量的关系用恒等式表示，即方程y=x，关系图也非常简单（见图6.11）。水管渗漏数据和这个恒等式类似，但是如果你把它们叠在一起，它们并不匹配（见图6.12）。

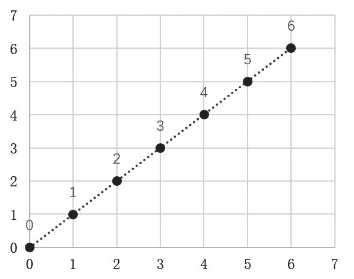
图6.11　“x=y”的图像

图6.12　图6.5和图6.11的比较

它们并不匹配的原因是，在我们水管渗漏数据集中，x项被乘以了斜率0.5。常数项（即y截距）在流量图和x=y图是匹配的，因为两者都是0，因此两根线都是始于坐标点（0，0）。然而，如果我们想让两根线完全匹配，我们需要改变函数x=y，使其斜率和流量数据图斜率相匹配。同时，如果流量数据图的y截距不是0，我们也需要把截距的数值加到函数x=y中。通过这样实现两条线的完全匹配。

给直线方程作图，使其可视化相对容易，因此我们不需要改变渗透流量研究的数据集。然而，有很多科学数据并不容易转化为图像或变得可视化，为了方便用函数表现现实中的变量关系，科学家使用多种技术来调整函数以拟合数据。按比例缩放和平移是两种常见的技术。

4.5.1　平移

为了移动一个函数，你需要在x或y变量上添加常数。

如果你在x变量上添加一个正的常数，整个线条会被向左移动。(www.xing528.com)

如果你在x变量上添加一个负的常数，整个线条会被右移。

如果你在y变量上添加一个正的常数，整个线条会被上移。在y变量上添加一个正的常数相当于在函数f（x）中减去一个正的常数。

如果你在y变量上减去一个正的常数，整个线条会被下移。在y变量上添加一个负的常数相当于在函数f（x）中添加一个正的常数。

4.5.2　比例缩放

当你缩放函数，需要将x或y变量乘以一个常数，从而实现将数据图的拉伸或者压缩。

如果你用大于1的常数乘以x，图就沿着x轴压缩。

如果你用小于1的常数乘以x，图就沿着x轴拉伸。

如果你用大于1的常数乘以y，图就沿着y轴压缩。用大于1的常数乘以y就相当于用函数f（x）除以那个常量。

如果你用小于1的常数乘以y，图就沿着y轴拉伸。用小于1的常数乘以y也相当于用函数f（x）除以那个常量。

我们怎样把x=y与水管渗漏数据相对应？我们已经知道，平移值是0（没有常数项b，因为我们是以空桶开始实验的）。比例因素是0.5，是图像的斜率。