使用移动平均值进行数据绘图

到目前为止，我们绘制的数据集都很简单，而且结果都是清晰的直线。如果我们每隔15分钟（即1/4小时），以十分之一升作为我们的精准度，更精确地测量第一个例子中的渗漏，会发生什么？我们可能会得到类似表6.4的数据集，数据图见图6.8。

我们现在收集的数据可能更精确，但是图就变得非常不规则。而且，在小段时间里的小变化可能并不能帮助我们回答问题（譬如渗漏流量有了变化可能是因为有人冲洗了坐便器，水管中的压力下降了），比如我们怎么计算出线条的斜率，更重要的是，怎么去掉小变化的影响？

表6.4　更精确的水管渗漏数据集

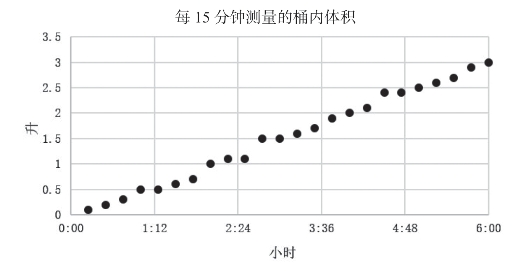
图6.8　更精确的数据集图像

在前面一章，我们讨论了多次测量同一个值，以使随机误差最小化。这在按时间序列进行的实验中无法做到，但是我们可以做类似的操作。我们绘图时可以用移动平均值（running average）取代各个测量值。

什么是移动平均？顾名思义，当你往下“移动”数据列表，可通过计算邻近数据的平均值作为移动的平均值。因此，对于我们上面的数据集，移动平均值可表示为表6.5中所示。

在该例中，我们用邻近的三个体积测量值算平均数，但是如果我们的数据集较大，或者量的变动很大，我们可以用更多的值。同时，为了计算简便，我们将数值精确到小数点后两位。

我们新数据的图像如图6.9所示。

虽然连接这些散点构成的线不会非常平滑，但它还是让我们更好地了解了体积变化的趋势，可以用来更准确地算出方程的斜率。(www.xing528.com)

我们可以通过连接图中的数据点画一条线，从而得到斜率的近似值（图6.10）（我们知道截距是0，因为实验的初始条件是空桶）。

沿着这些点画出的直线，斜率是0.5，因此移动平均的方程是y=0.5x+0，这与我们按小时测量得出的直线方程相同。

通过一条直线或曲线来表现数据集的过程称为曲线拟合（curve fitting）。

表6.5　水管渗漏更高精度数据集

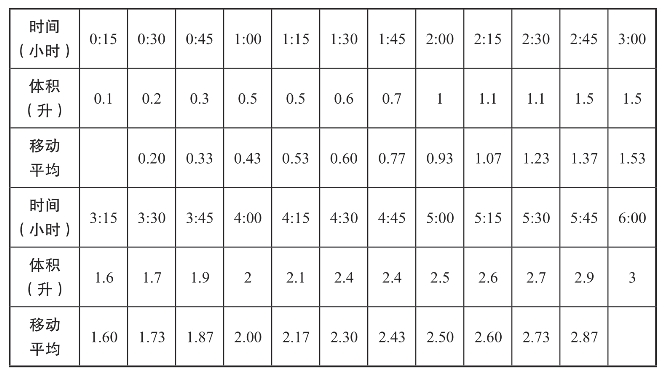
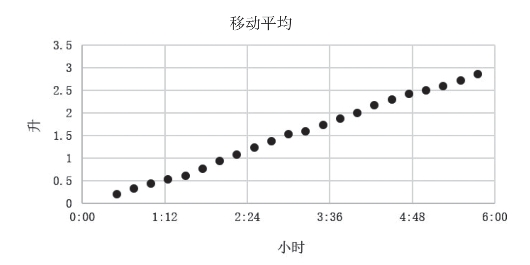
图6.9　移动平均数据图

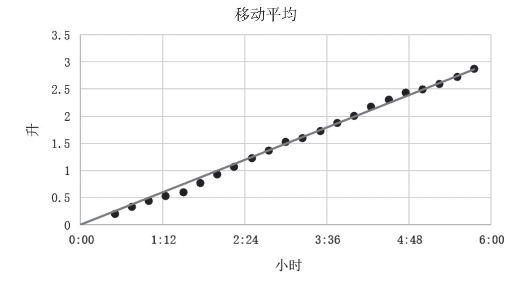
图6.10　曲线拟合示意图

我们将在后面深入讨论曲线拟合。