科学研究原理：重复测量的重要性

因为随机误差有时可能互相抵消，即使收集的数据有随机误差，科学家还是可以通过重复测量同一个值来发现正确的测量值。

例如，木匠丽莎试图锯8个单位长的木头，但是她在测量时有时少了一个单位，有时多了一个单位，有时准确。因为没办法预测丽莎用哪种方法测量，并且她测量得太长和太短的次数相同，这也许会被视作随机误差。

随机误差影响测量的准确，但是因为它们不是向一个方向偏差，也不是一直重复，可能生成围绕真实值的测量值集合。因此，即使有随机误差，你总是可以通过多次测量取平均值，得到准确的测量值，或者接近准确的测量值。研究者实际上预料到随机误差的发生，在设计他们的研究和分析时就已经考虑了这些误差。

让我们回到丽莎的例子。如果她打算锯8个单位长的木头（通过参考正确或真实的标准测量），她测量一次木头长度，可能得到的一个测量值是7、8或9。但是，她要是每段木头测三遍，把结果平均一下呢？她所有可能的结果是什么呢？我们可以画张表回答（表5.6）。

表5.6　测量结果可能性一览表

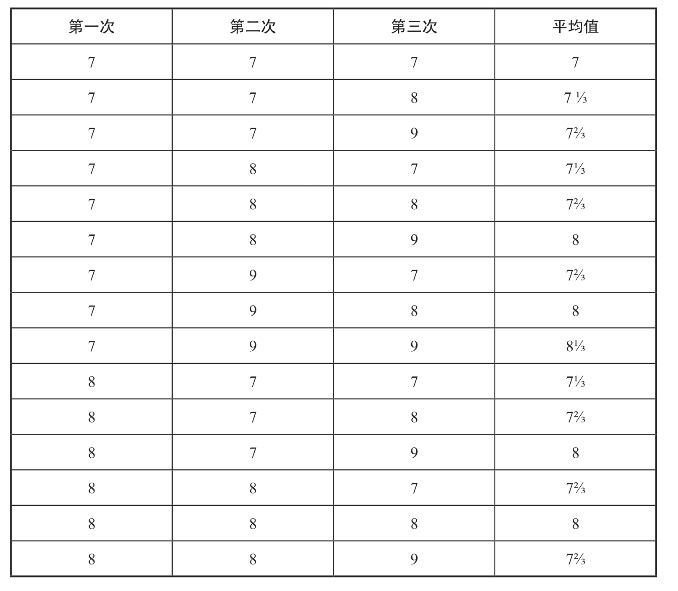
（续表）

如果丽莎只进行了27组测量（即表5.6的行数），每组获得三个测量值，她几乎不可能得到每种测量值的组合，即每种结果仅出现一次的情况。但是，随着她做越来越多组的测量，每种可能的测量值组合，即每种结果，多次出现的可能性就越大。

如果每次测量长度，得到7、8或9的可能性是相同的（1/3的可能性是7，1/3的可能性是8，1/3的可能性是9），我们可以通过根据它们的值，把结果放在一起做成图表：

只有一种方式使结果的平均值为7；

有三种方式使结果的平均值为7⅓；(www.xing528.com)

有六种方式使结果的平均值为7⅔；

有八种方式使结果的平均值为8；

有六种方式使结果的平均值为8⅓；

有三种方式使结果的平均值为8⅔；

只有一种方式使结果的平均值为9。

即使通过只测量三次取平均值，丽莎现在得到8个单位的准确测量结果的可能性更大，而不是得到不准确的7或9个单位。此外，再看那些包含分数的测量值——即使测量错误，还是更接近于8（正确的测量），而非7或9（不正确的测量）。通过多次测量，随机误差的影响可以最小化。

图5.7　测量结果的直方图

让我们进一步考虑这个测量问题。要是不采用每个长度测三次并取平均值的方法，丽莎把每个长度测十次并取平均值会怎么样？上面的表格宽度（即考虑不同可能的组合数量）将是310，即59，049。如果测量误差真的是随机的，也就是说，是7或9的结果的可能性与8一样大，图5.7中的中间部分的直方图会比之前高出更多，但是还是围绕着8。在10次测量后取平均值时，8还是最普遍的结果。然而，图表的两端，当10次测量平均值为7或9时，还是只有一种可能的组合。因为10次测量要得到平均值7或9，所有的测量值都必须是7或9。这种可能性是（1/3）10，即1/59049。对某个值的进行多次测量能得到更准确的结果。

但是，让我们更进一步探索问题的准确性。要是丽莎测量8个单位的结果不只是7、8或9会怎么样呢？要是她的误差是一个单位或两个单位的大小，测出结果是6、7、8、9或10会怎么样？上面的表或直方图会呈现出什么样子？如果测量值的范围是6—10，而非7—9，上面的表会有125列，即会有125种三个测量值不同的潜在组合。如果每个测量值仍有同样的可能性（现在变成1/5），图表也会宽得多，直方图的极值变成6和10，但是8还是图表中最高的部分，也是图表的中心。

随机误差可能导致测量值与被测量物体的实际值之间，存在或大或小的偏差。然而，如果真的包含随机误差，我们还是有可能通过重复测量得到一个真实（即正确）的值。

在下一章中我们将进一步讨论数据分析。