数据可以分成定性数据和定量数据两种，其中定量数据又可分为连续数据和离散数据。这些类别（如连续测量）可以继续细分，我们接下来探讨科学家描述数据的其他方式。
2.2.1 定类数据
当一个属性有数量有限的可能值，并且这些值的排列没有一定的顺序时，这类数据被称为定类数据或名义标度。在考虑定类数据时，你不能说一个值大于或小于另一个。定类数据是给我们要研究的事物分类，通常是离散数据，但是在一些特殊情况下可以是连续数据。
当数据描述的属性只能取两个值中的一个时，数据被称为二进制数。
如果我们的任务不是计数或测量黑色胶质软糖的重量，而是计算在盒中非黑色胶质软糖的比例该怎么办？首先，我们应该把盒子中的胶质软糖分成黑色的和不是黑色的两类。我们的结果看上去就像图4.2。
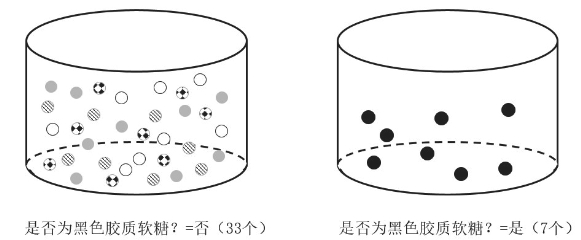
图4.2 分离黑色胶质软糖
对于盒子里的每颗胶质软糖，“它是黑色胶质软糖吗？”这个属性只有两个可能值：是或否。这个属性是二进制的。
非黑色胶质软糖的数量，即“是否是黑色胶质软糖？”的属性值为“否”的胶质软糖数量，是33。这个数量比上盒子里所有胶质软糖的数量是非黑胶质软糖的分数，即33/40。
那么如果除了胶质软糖，我们的盒子里还有带包装的糖果会怎么样呢？在这种情况下，属性可能是“这是哪一类糖果？”可能的值为带包装的糖果和胶质软糖。如果盒子里只有这两种糖果，那么属性也会是二进制的，因为没有其他可能的答案了。比如，对于“这是哪一类糖果？”属性，值为“胶质软糖”的糖果数量为10，值为“带包装糖果”的糖果数量为6。
二进制中一类特殊的数据是“是/否（true/false）数据”。它在计算机编程中被广泛使用。
假定你有一张关于棒球赛的数据表（表4.1）。
表4.1 棒球赛数据
你知道匹兹堡队是主队，洛杉矶队是客队。但是比赛日期还很遥远。我们知道比分吗？肯定不知道。我们不知道主队的得分，不知道客队的得分，也不知道哪支队伍赢了。我们想让这张表成立，我们需要为“我不知道”编码。
解决这个问题的一种方法是，在SQL数据库语言中，找到除了对和错外一个叫做空值（null）的值。SQL的逻辑被叫做三值或三进制逻辑。空值代表未知或者未定的数据，例如，未来棒球赛的比分，或者忘记输入的一个人的中间名。真值表中空值的运算规则与否（false）类似：如果空值与其他值进行数学运算，结果仍为空值。比如你想要计算数据库中每个主队得分的平均值，但是如果你的SQL命令碰到一场没开始或由于下雨而取消的比赛，平均值也是空值。
然而我们常常无法以二进制或三进制术语描述人类的特质，这里还有很多其他的值，我们不能简单地勾选未知项。“二元对立”长久以来都是我们文化的一部分，但是我们发现它们不能充分代表潜在的数据。我们需要的是种类更多的分类数据，而非二进制数据。
海吉拉斯
社会科学和医学研究中广泛使用的二进制数据之一是性别。性别这个属性被认为只有两个可能值——男性或女性。但是，在有些社会和文化中，其他性别被承认，而且事实上，在这些文化中生活的人们的确在这个属性上会有不同的取值可能性。
在印度，海吉拉斯被作为第三种性别而接受。公共文件和媒体把海吉拉斯描述成“中性”，而非男性或女性。在印度工作的医学研究者，他们在研究大众群体中的病人时，不能在他们的研究中用性别作为二进制数据。
无论过去还是现在，也有其他文化也承认第三（甚至第四）性别。美国的原住民把其他性别个体称为“双灵人”。
在我们的第一个胶质软糖例子中，我们有40颗5种不同花色的糖果。每颗胶质软糖有一个“花色”属性，那种属性的值是五种不同的可能性之一。如果我们为那些值建立一个数据库，它看上去有点像下面的表4.2：
表4.2 通过花色给胶质软糖分类
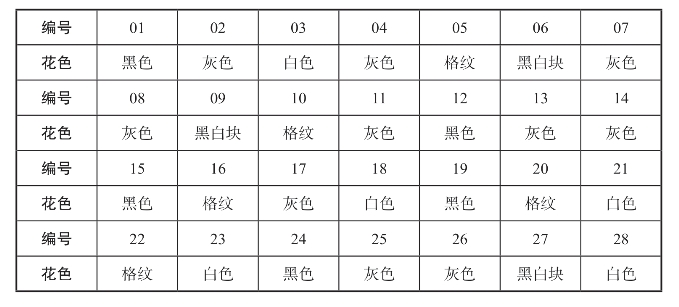
（续表）
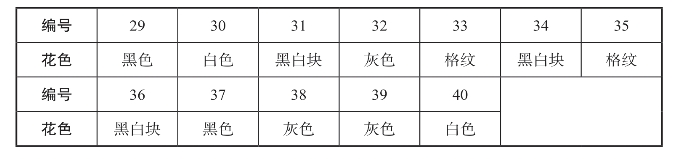
如果我们想根据花色把软糖分类，我们可以根据它们的花色属性，列出所有编号的胶质软糖，但是如果我们想把那些值按顺序排列，我们是做不到的：黑色胶质软糖不在灰色软糖之前，格纹的不在白色的后面（我们把胶质软糖编了号，让每一颗都有唯一的标识，我们也可以用字母编号，或者如果每颗糖都有唯一且不用保密的名字，我们可以直接使用它们的名字）。胶质软糖的花色是一种定类属性。(www.xing528.com)
2.2.2 定序数据
定序数据是有顺序的。也就是说，属性的可能值具有内在顺序。然而，这些可能值之间的准确差值并不能被测量。定序数据是典型的离散数据。
学生到教室挂起外套后，我们对每件外套进行字母编号会怎么样？如果字母是按字母顺序分配的，外套就会具有一个到达顺序（arrival order）的属性，它会告诉我们（以字母顺序），某件外套被挂到衣帽间的时间比其他外套早还是晚。然而，这个值并不会告诉我们外套挂上去的确切时间，也无法告诉我们那些外套被挂上的时间间隔：A外套可能是7∶45挂上去的，B外套是7∶46，C外套是8∶00。根据到达顺序编号而使用的字母值并不记录或传达这些信息。
定序数据对科学家有什么用？许多实验和研究过程涉及多个阶段。定序数据的价值之一是，能被用来记录研究对象处于哪个阶段。当科学家在对人进行研究时，他们可能对人们的受教育程度感兴趣。如果一份问卷调查让受调查者选择：没有受过正式教育／中学学历／大学肄业／大学学历／研究生或专业学位，那是否意味着高中学历是四年制大学学位的一半？不是的。但是我们知道大学毕业生比中学毕业生或大学肄业生学历层次更高。
定序数据也经常出现在其他种类的问卷调查研究中。社会学家经常要求研究对象评价他们对某事的感觉，或者对一个陈述的认同度。这类问题通常会被格式化为一系列选项：非常同意、同意、中立、不同意、非常不同意。这种按比例缩放的选项称为李克特量表。这种问题的结果是定序数据。
定序数据常与其他信息相关联。在上面的衣帽间案例中，外套被随机挂在任意挂钉上。如果学校要求学生依次从挂钩的一端往另一端挂外套，根据他们到达的顺序，包含到达顺序信息的字母值也会告诉我们外套在哪个挂钉上。
2.2.3 定距数据
如果数据的属性值等距分布，且该间距可被精确测量，这类数据被称为定距数据。在讨论定距数据时，除了用“第一、第二、第三……”，也可以用“一、二、三……”。间隔数据既可能是连续数据，也可能是离散数据。
以我们图4.1的数据为例，两层楼间的楼梯有15级楼梯。如果我们让15个人站在该楼梯上，每人站一级楼梯，他们站在哪一级楼梯上？这个属性的值不但会告诉我们每个人在哪一级，而且也会显示出他们相对于底楼的海拔。这是因为与定类、定序数据不同，定距数据能用于数学计算。
我们测出一层楼的高度是3.3米，有15级，均匀分布，楼梯顶部的高度可以通过先用3.3除以15，得到0.22米（一级楼梯的高度），然后用0.22乘以阶梯数。我们不但知道站在第五级台阶的人比站在第四级台阶的人高，而且知道站在第四级台阶的人高出地板0.88米（0.22乘以4），站在第五级台阶的人高出地板1.1米（0.22乘以5）。这些高度是定距数据。
定距数据有什么局限性？在上面的楼梯例子中，只需要用到我们现有的楼梯级数和楼层高度的知识，就能轻易地得出站在不同台阶上的人所在地高度。如果有人站在地板上，我们也能得出他与站在任何台阶上的人的相对高度，只需要把他的台阶数设为零。
我们用定距数据能得出人们在台阶上的相对高度。但是，我们可以说站在第四级台阶上的高度是站在第二级台阶上的两倍吗？不能。我们只能在“相对于地板”的前提下这么说。楼梯上的人相对于地平面的高度是多少？我们无从知道。
定距数据包含一个零点和所选择的整数值之间的间距。“所选择的”在这里是什么意思？在本章一开始的测量例子中，我们将温度作为连续数据的一个例子。当我们把温度计上显示的温度值定为26℃时，它也可以是26.1℃，或26.11℃等，这取决于我们设备的灵敏度。但是，同样的温度值也可以被定为79℉。这是怎么做到的？
华氏度和摄氏度都是定距尺度。也就是说，发明华氏和摄氏温度测量尺度（尺度这个词在这里指的是编号系统）的科学家们，把某一个温度设定为零点，用他们所选择的间距在温度计上标注其他的相对温度。
想象一个气象学家说本周温度比上周的温度高一倍，本周为80℉，因此上周为40℉。在摄氏温度中，本周温度是27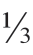
度，上周是4
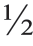度。4
度是27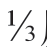
度的一半吗？不是的。这个“翻倍”的关系只适用于温度计上的数字，不适合“温度”这一被测量的实际属性。
2.2.4 定比数据
在相邻值之间的距离相等并且可被测量这一点上，定比数据和定距数据是相似的。相邻两个整数之间的实际间距是人为选择的（就像建筑师决定楼梯的每级台阶的高度）。然而，与定距数据不同的是，定比数据有绝对零点，它不取决于测量工具、测量尺度、实验设计或环境的任何其他因素。定比数据可以是离散数据，也可以是连续数据。一个物体的长度、重量和体积是典型的定比数据。
哈佛桥横跨麻省内查尔斯河，连接波士顿和剑桥，它剑桥的那端就在麻省理工学院的校园旁。桥长为2035英尺，或者说620.1米，也可以说是“364.4个斯穆特±一只耳朵”。“斯穆特”是一个非标准的长度单位。
在1958年，奥利弗·斯穆特是麻省理工学院的新生，由于一个恶作剧，“斯穆特”被兰博达兄弟会用作测量桥长的水平测距单位。这座桥那时就用“斯穆特”标记。每年兰博达兄弟会都重新粉刷这些标记，这个传统延续到今天。
奥利弗·斯穆特后来当上了美国国家标准局（American National Standards Institute，ANSI）和国际标准化组织（International Organization for Standardization）的主席。
说到温度，有一个测量尺度有绝对零值，就好比在楼梯这个例子中的地平面，它被称作开氏温标。在开氏温标上，“零”被定义为绝对零度（absolute zero）。绝对零度是理论上能达到的最低温度，它以物质基本粒子的能量限制为基础。绝对零度不由科学家人为设定，但是研究物理和相关领域的科学家们，在他们的计算中使用开氏温标的温度值（开氏温标的温度间距与摄氏温标一样）。如果气象学家声称根据开氏温标，本周比上周热了一倍，这个说法有数学意义（虽然也许不具备生物意义，因为那些气温可能不适合生存：60华氏度是15.6摄氏度、288.7开氏度）。
在定比尺度中，零值是不存在的，但有时会引入参照点（reference point）的概念。如果给水箱加水，工程师在测量那个水箱里水的体积，定比尺度下空的水箱就是零值。我们可以界定用于测量体积这个属性的标度（例如，它可能是升、加仑或者立方米），但是零值是由被测量的体系本身决定的。如果工程师声称今天的水位是昨天的两倍高，他的说法成立。
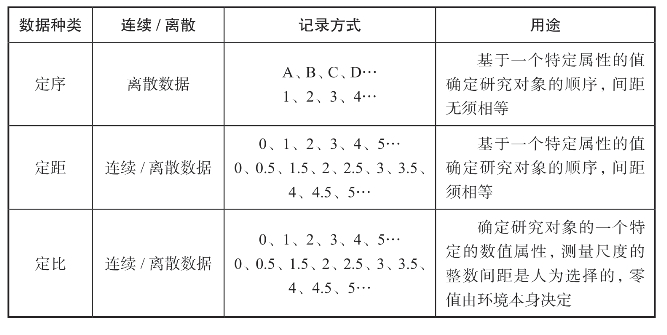
表4.3 数据种类和它们的用途
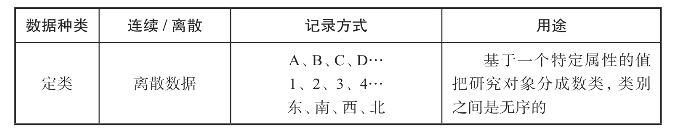
（续表）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
