中小学美术教育的均衡性理论模型及新论

首先,笔者对泰勒原理中的课程设计三大材料加以介绍,由此引出相应课程论学者为此所提出的相关理论模型;然后,就现有的理论模型进行反思,并详述坐标式模型的探索过程及其具体的内涵。

(一)课程设计中的均衡性理论简介

被誉为“现代课程论之父”的泰勒(Tyler)认为,从历史上看,有三种基本的材料依据已被人们用来作为进行课程决策的选择基础。它们分别为有组织的学科内容,接受课程内容的学生,以及社会。[2]

课程论专家钟启泉也认为,课程设计一般是指课程的组织形式或结构。课程设计基于两个层面:一是理论基础,二是方法技术。所谓理论基础,系指课程设计的三大基础——学科、儿童、社会。课程设计必须基于这三大基础,设计均衡课程。[3]4

可见,课程理论界对课程设计中使用的基本材料,公认的有三大材料:学科(subject)、儿童(child)、社会(society)。也有学者把其中的学科称为知识、把儿童称为学生,其实质是一样的。

课程设计中的均衡性理论主要是指:课程在设计上都应该建立在学科、儿童、社会这三大材料基础之上;三者之间通过相互联系与作用共同维持课程设计中的“均衡性”,以防出现极端化的课程;最终有助于课程目标的实现。

另外,笔者也发现,学术界似乎对“均衡性”的评判标准也没有一个明确定论。

总之,为了能更好地说明课程与三大材料之间的均衡性问题,下面笔者着重通过模型构建进行深入探讨。

(二)均衡性理论中的坐标式模型探究

关于模型。在现代教育科学研究方法中,模型的作用越来越大。所谓模型,就是认识并说明研究对象(原型),以便展开思考的独特的假设性构成物。所谓“建立模型”系指在某些关系上代表研究对象,提供关于研究对象的新知识,借助人造的或自然的系统(模型)间接认识事物的方法。总之,对不能直接认识的事物,以某种系统为媒介加以认识的一种方法,称之为“建立模型”。[4]

笔者下面将提出的“坐标式模型”系指上述达维多夫(Davydov)所认为的模型。

1．艾斯纳与三角形模型

20世纪70年代,美国斯坦福大学课程论专家艾斯纳在《儿童的知觉与视觉的发展》一书中针对“美术课程的侧重点”与学科、儿童、社会这三大材料之间的关系进行了图式化论述。尽管艾斯纳是从美术学科的角度来描述美术课程的侧重点问题的,但实际上这一问题与普通课程论中有关课程设计中的均衡性问题是一致的,都是基于对三大材料的共同思考。为此,笔者在下面的论述中给予一并使用。

艾斯纳认为,过去美术教育的各种侧重可以用一个三角形来表示。其中一个顶点代表以儿童为中心的观点,第二个顶点代表以社会为中心的观点,第三个顶点代表以学科为中心的观点。[5]艾斯纳还画出了说明不同教育偏重的示意图,如图2.1.1所示。

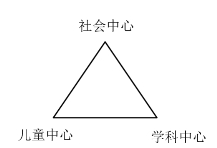
图2.1.1　三角形模型

从笔者所掌握的资料来看,艾斯纳似乎是最早采用三角形模型来图式化地论述课程设计中均衡性理论的研究者。

从另一方面来看,笔者认为艾斯纳三角形模型主要有以下两点不足。

首先,该模型没有“课程”标识,以至于模型设计显得不够完整。例如,我们仍需借助文字来描述课程这一维度是如何在三大基点之间取得平衡的。

其次,该模型不能揭示课程与三大基点之间的动态关系。三角形模型是静态的、封闭的。在后现代课程观视角下,课程应具有不确定属性,三大基点也是不能被封闭的,因为它们都会随着时代的进步而不断延伸,在动态生成中来获得平衡,从而得以不断发展。

2．国内相关研究者对类似问题与模型的讨论

1989年,上海市中小学课程教材改革委员会主任王生洪教授率先推出了“以社会需求、学科体系和学生发展为基点,以提高学生素质为核心”的三角形素质教育课程设计模型。钟启泉认为,所谓课程设计教育学模型无非是将各种制约课程设计的因素加以简化,借助图像式或符号式表述明示其构成要素及其相互关系的一种方法。[6]

笔者纵观全文,发现钟启泉没有明确标示出关于三角形素质教育课程设计的具体模型。笔者估计钟启泉所认为的三角形很可能也是类似于艾斯纳提出的上述图示。

因为国内课程理论界对课程设计均衡性模型的研究不多,所以笔者也很难再查阅更多的相关文献来进一步说明这一方面的研究成果。

3．构建美术课程设计中的“坐标式模型”

基于艾斯纳三角形模型设计中的不足,笔者引入数学研究中常用的坐标系来进行重新构建,以求能充分呈现课程设计与三大材料之间的逻辑关系。

笔者构建的下图2.1.2即为“坐标式模型”。所谓坐标式模型是特指基于数学中的立体坐标系来研究美术课程与三大材料之间均衡性问题的模型。笔者提出的“坐标式”,是基于美术课程(curriculum)、美术学科、儿童、社会这四大方面的特殊关系,采用类似于数学中的三维坐标轴,将它们统一在一个坐标系中的图式化模型。

这里需要说明的是:虽然美术课程与三大因素之间的关系不能用定量的方法来研究它们之间的具体数值;但可以参考自然科学中的“标量”特性,即只注重其方向与作用点而不强调其大小,来研究四者之间的关系。所以说“坐标式”只是借用其名称,吸取其有益成分,而不是完全依照数学中的坐标规则来构建模型。

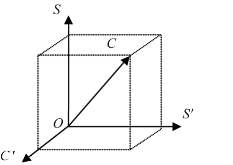
图2.1.2　坐标式模型

图2.1.2中,C为英语“课程”单词curriculum的第一个字母,类似地将“学科”用大写字母“S”来表示,“儿童”用“C′”,“社会”用“S′”;如此图中OC、OS轴、OC′轴、OS′轴则分别代表美术课程、美术学科知识、儿童、社会。依据四者的关系,从纯数学理论来研究的话,在某一历史时刻t,它们之间的关系可以用函数表示为C＝f(s,s′,c′,t)。值得注意的是,如上所述,人文学科中的这四个要素是不能被定量的,即“对应关系f”是不太可能被具体确定的。为此,笔者把上述函数式改写为C∝f(s,s′,c′,t),其中∝表示“相关性”。(www.xing528.com)

笔者认为,坐标式模型至少能充分解释美术课程均衡性理论中的下列问题。

第一,该模型能解释美术课程设计的均衡性。从数学意义上来说,美术课程与其他三个坐标轴之间都成45°时就是均衡的。图2.1.2就是美术课程与三大因素之间形成45°角的图式,即均衡性图式。

第二,该模型能解释美术课程设计的偏向性。以下三幅图对美术课程基于不同偏向给出了形象化描述。图2.1.3说明美术课程基于美术学科偏向,这时课程维度所形成的长方体明显偏向S轴;图2.1.4说明美术课程基于社会偏向,这时课程维度所形成的长方体则明显偏向S′轴;图2.1.5说明美术课程基于儿童偏向,此时课程维度所形成的长方体则明显偏向C′轴。

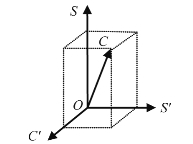
图2.1.3　偏向美术学科

图2.1.4　偏向社会

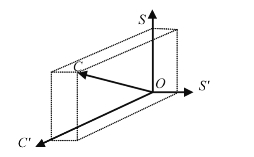
图2.1.5　偏向儿童

第三,该模型能解释美术课程设计的极端性。图2.1.6说明美术课程完全基于学科知识的设计,课程OC与OS轴重合;图2.1.7说明美术课程完全基于社会因素的设计,课程OC与OS′轴重合;图2.1.8说明美术课程完全基于儿童经验的设计,课程OC与OC′轴重合。这些美术课程设计都是极端化的,是人们在设计中应该尽量避免的。

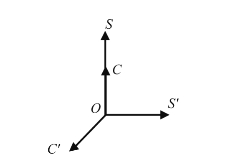
图2.1.6　与美术学科重合

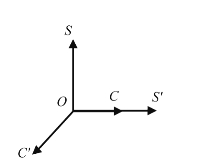
图2.1.7　与社会重合

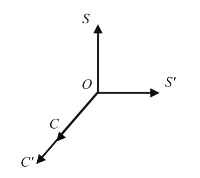
图2.1.8　与儿童重合

综上所述,笔者认为坐标式模型无论从图式的逻辑上还是美学上,都比三角形模型更能解释美术课程设计的均衡性理论问题。

4．美术课程设计如何获得均衡性

笔者从以下两点来思考这一问题。第一,定量意义上的静态均衡性。如上所述,从纯数学的角度来看,美术课程维度与其他三个材料之间都成45°,就能严格保证均衡性,如图2.1.2所示。

第二,定性意义上的动态均衡性。即课程维度是在定量静态均衡点,成45°时周围进行振荡,来获得随机的动态均衡。这一点在理解上需要我们有统计学的相关背景知识。

笔者认为,在实际教学中,美术课程维度不太可能处于纯数学意义上的“绝对均衡的终极理想点”上;而应该稍微具有偏向性,并在一定的“值域”内进行振荡,通常处于定性意义上的一个动态范围,但总体来看却是均衡的。

当然,至于如何在操作层面来获得均衡,这需要笔者今后做进一步的理论与实践探索。

二、美术新课程中的异化问题罗列

(一)美术新课程的异化现象

虽然从2001年7月国家颁布《全日制义务教育美术课程标准(实验稿)》以来,全国各地中小学在美术教学形式的多元化、丰富性等方面出现了前所未有的喜人景象,但同时也暴露出当下美术教育界争议颇多的所谓“游戏性”“空壳性”“替代性”“形式化”“杂耍课”“浮华病”“泡沫化”[7 8]等过于偏离美术新课程目标的混乱现象。有研究者将这一现象归结为“美术课程的异化”[7]。

(二)美术新课程的异化分类

笔者认为上述异化现象可以大体分为两大类:一是主要偏向于学生维度的“游戏性”“杂耍课”等现象;二是主要偏向于社会维度的各类“形式化”教学模式。诸如“空壳性”“浮华病”“泡沫化”等异化现象,则是这两种类型的混合。

(三)美术新课程的异化实质

笔者认为异化的实质之一是绝大部分的普通教师由于严重缺乏课程理论知识,根本不了解课程设计中的三大基本材料,以及课程设计中的均衡性问题,从而导致了美术课程设计的不均衡性普遍存在。当然,这类教师群体也包括一部分编写美术教科书案例的所谓的骨干教师及学科带头人。如果我们仔细推敲他们编写的课例,就会发现其中也存在着严重违背均衡性的重大问题。

(四)美术新课程的异化后果

最严重的后果是美术课程设计的极端化。如果这一现象不能及时得到纠正,很可能会在美术新课程中出现类似以往“技法中心论”“学生中心论”“社会中心论”课程,并进一步蔓延。这就很可能会导致美术新课程改革深陷泥潭而难以自拔。