混业经营中二元Copula参数估计的研究成果

上面的小节中已经给出了边际分布函数中各参数的估计值，要得到相依情形下总体操作风险的值，还要先对前面给出的三种不同二元Copula的参数进行估计。根据上一章给出的各Copula参数估计的方法和步骤，利用内部欺诈一年期总体损失和外部欺诈一年期总体损失的样本数据，得到基于不同方法的二元t Copula、二元Gumbel Copula和二元Clayton Copula各参数的估计值如表6-8所示。

表6-8　基于不同方法的不同二元Copula的参数估计值

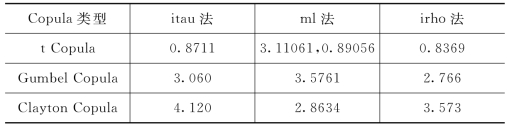
该表列出的三种方法中，itau表示Kendallτ反函数法，ml表示极大似然估计法，irho表示Spearmanρ反函数法。其中，二元t Copula模型在ml法下得到的两个参数估计值分别为自由度ν的估计值及其相关系数矩阵中两个变量之间的相关系数ρ的估计值，由于对二元t Copula中自由度参数ν的估计只用了极大似然估计法，故这里只在ml法下给出了其参数估计的值。对于其他各参数来说，由于每种方法下得到的参数估计值都不一样，因此，这里首先对各参数在不同估计方法下得到的不同估计值所对应的标准差取倒数，再以每个倒数在所有倒数和中所占的比例作为该参数在不同方法下得到的估计值的权重，最后将不同方法下得到的不同参数估计值与其对应的权重相乘再求和，并以该加权和作为该参数最终的估计值。也即，设参数θ在三种不同估计方法下得到的参数估计值分别为^θ1，^θ2，^θ3，这三个估计值对应的标准差分别记为a1，a2，a3。为了确定最终的参数估计值，将上述估计值和标准差按照下面的步骤进行处理：

（1）分别对三种方法下各估计值对应的标准差求倒数，即分别令b1=1/a1，b2=1/a2，b3=1/a3；

（2）分别令c1=b1/（b1+b2+b3），c2=b2/（b1+b2+b3），c3=b3/（b1+b2+b3），即可得到各参数估计值的权重c1，c2，c3；

（3）将不同方法下参数的估计值与上述权重的乘积相加得到参数的最终估计值，即令，即可得到参数θ最终的估计值。

表6-9给出了基于不同方法的不同Copula模型中各参数估计值的标准差，其中二元t Copula模型在不同方法下的标准差值指的是该模型中参数ρ在不同方法下的估计值对应的标准差值。

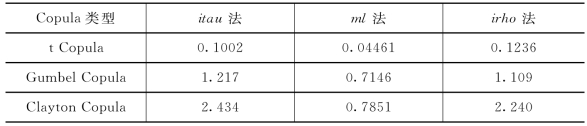
表6-9　基于不同方法的参数估计值的标准差

(www.xing528.com)

表6-9中各值分别为表6-8中各参数估计值对应的标准差值。

根据上面介绍的方法和步骤，得到各二元Copula在不同方法下参数估计值对应的权重分别如表6-10所示：

表6-10　不同方法下参数估计值的权重

续　表

表6-10中各值分别为表6-8中各参数估计值对应的权重。由上面给出的权重计算方法，以及该表中各权重的值与表6-9中各标准差的值相对照可知，参数估计值的标准差越大，其在最终参数估计值的计算中所占的权重越小；相反，参数估计值的标准差越小，其在最终参数估计值的计算中所占的权重越大。由于在参数估计的过程中，估计值的标准差越小，表明该估计值的有效性越好，因此，上面的方法相当于根据各不同方法下参数估计值的有效性对其进行加权，有效性越好的估计值权重越大，有效性越差的估计值权重越小。

根据上述权重以及前面给出的方法，得到不同二元Copula模型中各参数的估计值如表6-11中所示。

表6-11　不同二元Copula模型的参数估计值