混业经营中金融风险度量研究

在考虑内外部欺诈间的相关关系时，通常要考虑的相关关系有两种，一种是相互独立，一种是相互不独立。在独立情形下，对总体操作风险一般采用传统的方法进行度量；在不独立的情形下，一般都利用Copula函数来对它们之间的关系进行描述。下面首先给出独立情形下总体操作风险的度量。

根据前面的介绍，内部欺诈损失强度Xi的分布函数F1（x）以及外部欺诈损失强度Yj的分布函数G1（y）均属于次指数分布族，且在对总体操作风险进行度量的过程中，有如下假设条件：内部欺诈损失强度｛Xi，i∈ℕ｝与外部欺诈损失强度｛Yj，j∈ℕ｝均为独立同分布的变量，且他们分别与内部欺诈损失频度N1和外部欺诈损失频度N2相互独立。由前面的计算可知，

当假设内部欺诈和外部欺诈之间相互独立（也即L1和L2之间相互独立）时，操作风险总体损失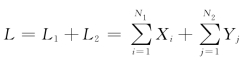的分布函数Φ（z）的生存函数可以表示为

故由（5.3.17）和（5.3.18）式可得，在假设内部欺诈和外部欺诈相互独立，且内部欺诈损失强度和外部欺诈损失强度的分布函数F1（x）和G1（y）之间也相互独立的情形下，对于足够大的z，操作风险总体损失分布函数的生存函数可以表示为(www.xing528.com)

由前面的计算可知，分布函数F1和G1均为Pareto分布，因此，由Embrechts等（1997）给出的引理可以得到，当这两个分布函数的自变量足够大时，由

且将其代入式（5.4.4）中可得，对足够大的z，有

结合前面给出的内部欺诈损失强度分布函数F1（x）和外部欺诈损失强度分布函数G1（y）的近似解析式可知，在内外部欺诈相互独立的情形下，一年期内外部欺诈总体损失分布函数的近似解析表达式为：