金融风险度量的数学描述及相关研究

就如前文所说，在研究操作风险的度量问题时，是在考虑内外部欺诈之间的相关关系的前提下进行的。因此这里要对内部欺诈导致的操作风险损失分布和外部欺诈导致的操作风险损失分布，即边际分布分别进行讨论，最后再在考虑它们之间相关关系的基础上得到最后总体操作风险损失的分布函数，进而求得最终的以VaR为度量工具的操作风险值。

为了对所研究的问题进行更清楚的表述，用Xi表示由内部欺诈导致的每次操作风险发生时的损失，也称为内部欺诈损失强度；用Yj表示由外部欺诈导致的每次操作风险发生时的损失，也称为外部欺诈损失强度；用N1表示一年期由内部欺诈导致的操作风险损失发生的次数，也称为内部欺诈损失频度；用N2表示一年期由外部欺诈导致的操作风险损失发生的次数，也称为外部欺诈损失频度。则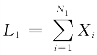表示一年期由内部欺诈导致的操作风险损失总和，也称为一年期内部欺诈损失变量或内部欺诈总体损失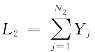；表示一年期由外部欺诈导致的操作风险损失总和，也称为一年期外部欺诈损失变量或外部欺诈总体损失。一年期由内部欺诈和外部欺诈导致的操作风险损失总和，也即一年期操作风险的总体损失变量表示为

记Xi的分布函数为F1（x），Yj的分布函数为G1（y），L1的分布函数为F（x），L2的分布函数为G（y）。假设｛Xi，i∈ℕ｝与｛Yj，j∈ℕ｝均为独立同分布的随机变量序列。同时，假设｛Xi，i∈ℕ｝与N1之间相互独立，｛Yj，j∈ℕ｝与N2之间也相互独立。

本章的主要目标就是在上述假设条件的基础上，对混业经营下操作风险度量的模型和方法进行探讨。利用特定的模型和方法，得到混业经营下操作风险总体损失变量L的分布函数，再根据得到的分布函数以及VaR的定义得到最后的操作风险值。记操作风险总体损失的分布函数为Φ（z），则(www.xing528.com)

即最终的目的是通过求得上式所表示的Φ（z）的值，得到最后的操作风险值。

本章中对总体损失分布函数的求解步骤如下。首先，分别得到L1和L2的分布函数，即边际分布函数的解析表达式。由于Xi，Yj，N1以及N2均为随机变量，故根据上述L1，L2的表达式可知，L1，L2均为随机变量的随机和。因此，对其分布函数的求解也即为对随机和分布函数的求解。其次，在得到L1，L2的分布函数后，再在考虑内外部欺诈之间相关关系的基础上，得到最后的总体损失L的分布函数，最后根据VaR的定义得到最终操作风险的值。当然，在求解边际分布函数之前，首先要考虑的是独立同分布随机变量序列｛Xi，i∈ℕ｝和｛Yj，j∈ℕ｝的分布函数F1和G1的求解，以及损失频度随机变量N1和N2的分布函数的求解。

对边际分布函数，即内、外部欺诈总体损失L1和L2的分布函数进行求解的方法和模型有很多，根据这些不同方法和模型的特点，下面将对其中基于一阶近似的边际分布函数求解（简称为基于一阶近似的分布函数求解）、在一阶近似的基础上进行均值修正的边际分布函数求解（简称为均值修正的分布函数求解）以及基于二阶近似的边际分布函数求解（简称为基于二阶近似的分布函数求解）等几种不同类型方法和模型进行简单的介绍。其中，基于一阶近似的边际分布函数求解以及基于均值修正的边际分布函数求解方法主要借鉴于丰吉闯（2012）中介绍的基于一阶近似和均值修正模型的操作风险计算方法。由于本文是在考虑内、外部欺诈之间相关性的基础上来对总体的操作风险度量进行研究的，因此，这些对边际分布函数（即对内部欺诈总体损失分布函数和外部欺诈总体损失分布函数）进行求解的方法和模型，也可以用于在不考虑内外部欺诈相关性的情形下，对总体的操作风险的度量进行研究。