本节中对数据的分析及模型的参数估计都是通过R软件实现的。作为数据分析结果的各股票日对数收益率数据的描述性统计特征表在此处就不一一呈现,而只给出根据各描述性统计特征得到的结论。
根据各股票数据的统计特征可以得出,上述8只股票日对数收益率数据的偏度明显,峰度也较高。J-B检验表明,每只股票日对数收益率数据都在1%的显著性水平下拒绝正态分布假设。LM检验证明所有的对数收益率序列都有明显的ARCH效应,再根据前面所说的金融收益时间序列数据一般都具有异质性和自相关性。因此,这里选用ARMA(1,1)-GARCH(1,1)模型对各对数收益率序列进行拟合,再将通过过滤得到的独立同分布标准残差序列利用经验分布函数法转化为服从标准均匀分布的随机变量,最后再进行C藤Copula函数的参数估计。为了方便表述,将8只股票按如下编号:神火股份(V1),冀中能源(V2),中金岭南(V3),中联重科(V4),万科(V5),招商地产(V6),宏源证券(V7),宁波银行(V8)。
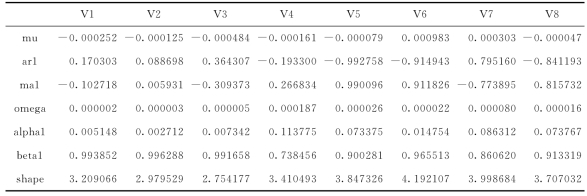
首先,利用ARMA(1,1)-GARCH(1,1)模型对各股票的对数收益率进行估计,得到的参数估计结果如表4-1所示中给出。在对各股票对数收益率序列进行ARMA(1,1)-GARCH(1,1)建模后,还需要对经过该模型过滤之后的残差收益率序列进行自相关检验。根据自相关检验的结果可得,经过ARMA(1,1)-GARCH(1,1)模型滤波之后的标准化残差序列不存在一阶自相关和二阶自相关。另外,对标准化的残差序列做概率积分变换,并利用K-S检验方法对其进行检验,得出变换后的序列服从(0.1)上的均匀分布的结果。因此,对上述8只股票的日对数收益率采用ARMA(1,1)-GARCH(1,1)建模是有效的。
表4-1 ARMA(1,1)-GARCH(1,1)模型的参数估计结果
根据前面章节所描述的方法,得到C藤Copula模型中各树形图的根节点顺序为:V3,V7,V6,V5,V2,V8,V4,V1。基于AIC准则选择的双变量Copula函数及这些Copula函数对应的参数如表4-2~4-8所示。确定最优的双变量Copula后,根据极大似然估计法估计出的参数值,计算得到的相应Kendall′τ秩相关系数也在各表中给出了。其中,旋转180度得到的Copula称为survival Copula。如旋转Clayton Copula 180°后得到的Copula称为Survival Clayton Copula。表4-2~4-8中的第一列指的是每棵树中与两节点相连的边的名称,如V1,V3表示节点V1与节点V3相连的边,V1,V7|V3表示节点(V1,V3)与节点(V7,V3)相连的边,V1,V6|V7,V3表示节点V1,V7|V3与节点V6,V7|V3相连的边,以此类推。上一棵树中的边为下一棵树中的节点。par及par2分别表示Copula函数的参数1和参数2,对于只有一个参数的Copula函数,只有一个参数par。此外,运用上述方法得到的样本数据C藤结构图中的第一棵树形图也在如图4-2所示中给出了。图4-2中方框内表示各个节点,连接两个节点的边上分别为这两个节点之间的Pair-Copula及其对应的Kendall'τ系数。类似地,还可以得到其C藤结构图中的第二、三、四、五、六、七棵树形图,在此就不一一给出。
表4-2 第一棵树的相依结构
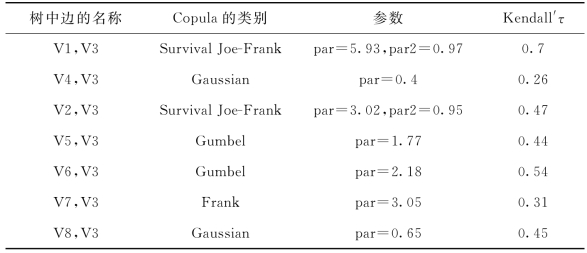
表4-3 第二棵树的相依结构

表4-4 第三棵树的相依结构
 (https://www.xing528.com)
(https://www.xing528.com)
续 表

表4-5 第四棵树的相依结构

表4-6 第五棵树的相依结构

表4-7 第六棵树的相依结构

表4-8 第七棵树的相依结构

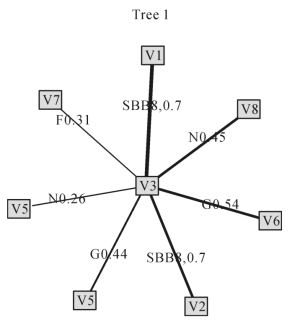
图4-2 样本数据的C藤结构图的第一棵树形图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




