显然，对于高维随机变量的分布函数来说，其pair-Copula结构不是唯一的，而是有多种可能。为了对多元随机变量之间的这种相依结构进行系统的描述，学者们引入了一种被称为规则藤（Regular Vine）的图解模型。根据上面对pair-Copula结构的描述可知，规则藤的类是很大的，其中包含了多元随机变量分布函数所有可能的pair-Copula结构。也可以说，规则藤是一种表示多元随机变量中各分量间pair-Copula结构的图解模型，该模型将多元随机变量间所有可能的pair-Copula结构包含在内。因此，也可以将其看成是包含所有可能pair-Copula结构的类。由于该图解模型的建立是以pair-Copula为基础的，且其主要目的是以Copula密度函数与各单变量分布密度函数相结合的方式对多元随机变量之间的相依关系进行描述，故将其称为规则藤Copula模型。当然，用规则藤Copula模型对多元随机变量中各单变量之间的pair-Copula结构进行描述的方式也不是唯一的，不同的描述方式对应的藤Copula模型和结构不同。下面分别从文字描述和结构图两个角度对各藤Copula模型的定义及其性质进行简单的介绍。
首先，对R藤（Regular Vine）Copula模型的结构进行简单的描述。R藤（R-Vine）Copula模型是最一般的藤Copula结构模型。除此之外，还有C藤（Canonical Vine）、D藤（D-Vine）Copula模型。对R藤Copula模型结构的描述可以概括为以下几点：
（1）每个n维藤Copula都由n-1棵树来表示；
（2）第j棵树具有n+1-j个结点和n-j条边；
（3）每棵树中的每条边对应的是一个双变量Copula密度函数；
（4）第j棵树中的边是第j+1棵树中的结点；
（5）第j棵树中同一个结点连接的两条边在第j+1棵树中是由一条边连接的两个结点；
（6）整个藤Copula结构由
条边（也即
个双变量Copula密度函数）和边际密度函数来定义，也即这两者确定了一个藤Copula结构。
对C藤Copula模型最简单的定义就是：每棵树都有唯一的一个结点与n-j条边相连的R藤Copula模型。也就是说，C藤Copula模型可以看成是R藤Copula模型的特例。类似地，D藤Copula模型也可以看成是R藤Copula模型的特例。对其最简单的定义就是：每棵树都没有任何一个结点与多于两条边相连的R藤模型。为了更好地对藤Copula模型的结构特征进行说明，下面采用图形与公式相结合的方式分别对五维C藤和D藤Copula模型的结构进行描述。(www.xing528.com)
首先，分别令
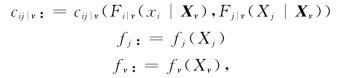
对五维C藤Copula模型来说，有
f12345=f1·f2·f3·f4·f5·c12·c13·c14·c15·c23｜1·c24｜1·c25｜1·c34｜12·c35｜12·c45｜123，
对五维D藤Copula模型来说，有
f12345=f1·f2·f3·f4·f5·c12·c23·c34·c45·c13｜2·c24｜3·c35｜4·c14｜23·c25｜34·c15｜234.
对应的五维C藤和D藤Copula模型的结构如图4-1所示。其中，图4-1（a）为五维C藤Copula模型结构图，（b）为五维D藤Copula模型结构图。
图4.1 五维C藤（a）和D藤（b）树形图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
