混业经营下金融风险度量的建模思路及模型简介

本章研究的是混业经营下金融机构或者金融主体所面临的市场风险的度量，根据聚合风险的定义以及混业经营下金融机构或者金融主体经营和拥有的基础金融产品的特征，也可以将其看成是对聚合风险的度量。前面已经有过比较详细的介绍，在混业经营的模式下，各金融机构或者金融主体所拥有和经营的金融产品的种类增多，且每种金融产品所包含的基础金融产品数量也有很多。也就是说，其面临的市场风险包含了数量庞大、相互之间的关系错综复杂的基础风险因子。为了对这些风险因子的总和，即聚合风险进行准确的度量，故建立以下模型。

该模型建立的大体思路如下：首先，按照所属的金融产品类型将所有基础风险因子（即基础金融产品收益率）进行分类。然后，对各组基础风险因子进行求和，得到各组风险因子的子和，并对其分布函数进行求解。最后，以上述子和为新的风险变量，对所有这些子和风险变量进行求和，得到总体风险（即聚合风险）分布函数的界。依据该思路，将聚合风险S写成下列形式：

式中，N表示混业经营下金融机构或者金融主体所拥有的不同类型金融产品的种类数，ni表示第i种类型金融产品中所包含的基础金融产品的个数，Xik表示属于第i种类型金融产品的第k个基础金融产品收益率，也称为第k个基础风险因子。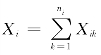，i=1，2，…，N。根据前面对本章所研究问题的描述，各基础风险因子的分布函数是已知的，用｛Fik：i=1，2，…，N，k=1，2，…，ni｝表示，但是它们之间的相依关系是未知的，这种未知的相依关系用CS表示。

与已有的研究中对基础风险因子之间的相依关系进行处理的方式不同，这里采用多个不同的较低维Copula函数来代替传统聚合风险研究中的一个较高维Copula函数来对所有基础风险因子之间的相依关系进行度量。所谓的较低维和较高维指的是，与传统聚合风险度量的研究中，仅使用某一个Copula函数来对所有基础风险因子之间的相依关系进行度量的方法不同，这里所用的模型和方法是：对所有的基础风险因子分类后，采用不同的Copula函数对每组内基础风险因子之间的相依关系进行度量。因此，该模型和方法中用到的Copula函数的维数较传统方法中用到的Copula函数的维数要低，传统方法中用到的Copula函数的维数较本章混业经营情形下所用模型中Copula函数的维数要高。

用｛CX，CXi，i=1，2，…，N｝分别表示N+1个风险因子向量（X1，x1…，XN），，，…，的Copula函数，则传统方法中的维Copula函数CS被N维Copula CX以及ni维Copula｛CXi，i=1，…，N｝代替。由于每组基础风险因子｛Xi，1，…，Xi，n1｝（i=1，2，…，N）都属于同一种类型的金融产品，因此，属于不同类型金融产品的各组内基础风险因子之间的相依关系应该是不同的。这些不同的组内基础风险因子之间的相依关系分别用Copula｛CXi，i=1，2，…，N｝来表示。即CXi表示第i组内各基础风险因子之间的相依关系。对每组内各基础风险因子进行求和后，分别得到各子和形成的新风险变量｛X1，X2，…，XN｝。这些新的风险变量分别代表了不同类型金融产品的风险，因此，它们之间的相依关系与属于同一类型金融产品的各基础风险因子之间的相依关系是不一样的。从另外一个角度，这些因子和形成的新风险变量之间的相依关系属于基础风险因子组间的相依关系，而同一类型金融产品内各基础风险因子之间的相依关系属于基础风险因子组内的相依关系，组间的相依关系与组内的相依关系通常都是不一样的。用Copula函数CX表示各子和形成的新风险变量之间的相依关系。为了更好地对该模型进行理解，下面给出一个简单的例子。(www.xing528.com)

假设混业经营下某金融机构或金融主体所拥有或者经营的基础金融产品来自股票、债券以及基金3个不同的金融产品类型，即N=3。其中每种类型金融产品所包含的基础风险因子的数量分别为n1，n2和n3。这些基础风险因子分别用变量X11，…，，X21，…，，X31，…，来表示，它们可以看成是基础金融产品的收益率或者损失等。在假设所有这些基础风险因子的分布函数已知，但其相依关系未知的情况下，记金融机构或者金融主体所面临的市场风险为e（S），其中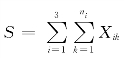，为所有基础风险因子的总和，e为某种风险度量工具。本文采用的风险度量工具为VaR。

根据上述模型建立的思路和方法，在对这种情形下金融机构或者金融主体所面临的市场风险（按照前面所述，也可以称之为聚合风险）进行度量时，首先将所有的基础风险因子按照它们所属的金融产品类型分成三组，每组用向量表示出来分别为：（X11，…，），（X21，…，）以及（X31，…，）。与传统聚合风险研究中对基础风险因子间的相依关系进行处理的方式不同，这里先对每组基础风险因子和的分布函数进行求解，即分别得到所有股票类、所有债券类和所有基金类基础风险因子和的分布函数。再用X1，X2，X3分别表示对每组风险因子求和后得到的新的风险变量，其分布函数分别为上述求得的三种不同类型金融产品内各基础风险因子和的分布函数。最后对三种新的风险变量和的分布函数进行求解，即可得到所有基础风险因子和的分布函数及其对应的风险VaR值。在计算的过程中，利用四种低维Copula函数分别对新的风险向量（X1，X2，X3）和不同组内基础风险因子随机向量（X11，…，），（X21，…，）以及（X31，…，）中各分量之间的相依关系进行描述。而不是像传统聚合风险度量中那样，利用一个高维Copula函数来对所有的基础风险因子X11，…，，X21，…，，X31，…，之间的相依关系进行描述。

由前面对混业经营下金融机构或者金融主体所拥有或者经营的基础金融产品收益率之间相依关系的分析可以看出，该分组模型是基于实际情况建立的。它不仅与所研究的实际情形更相符，而且还可以避免使用高维Copula函数时出现的“维数灾难”问题。在实际操作中，所有基础风险因子的分布函数可以通过曲线拟合或者极大似然估计的方法进行求解。对所有未知的Copula函数，可以利用经验Copula来代替真实的Copula，然后根据与后面给出的模拟算法类似的计算过程得到最终的结果。