混业经营下金融风险度量的相关研究

迄今为止我们已经讨论了单期损失的分布及相应的风险度量问题。很多情况下，我们需要通过单期损失的风险度量模型推出针对多期损失分布的风险度量模型。例如，假设我们对日风险因子变化进行建模，以便对日VaR和预期亏损的值进行计算。同时，我们也想要得到交易组合在该时间段内保持不变的假设条件下，一周或者一个月损失分布的VaR和ES估计值。

显然，我们可以将风险因子变化的多期日数据聚集起来得到频率较低的风险因子变化数据，再利用这些数据得到上述一周或一个月损失分布的一期估计值。这会导致数据量的减少，同时也需要对聚集的数据进行额外的分析。对于前一个问题，可以通过构造重叠的风险因子收益来解决，但我们并不推荐这种方法，因为这需要对数据序列间的相关性进行度量，从而极大地增加统计建模的复杂度。

缩放。若能找到将单期风险度量转化为h（h＞1）期风险度量的简单规则，这对所有风险管理者来说都具有极大的吸引力。将从时刻t开始，到时刻t+h之间的损失用来表示，则有

其中，表示在t时刻时间区间为h的损失算子。但是怎样将风险度量应用到跨越了h个时间段的损失的分布中去，除了一些特殊的例子外，该问题还没有合适的解决方案。

若风险度量的映射很明显地依赖于时间（如衍生品交易组合），则h期的损失算子与一期的损失算子不同。为了简化，我们假设映射不依赖于时间，即有。则该算子的线性形式为，其中bt在时刻t已知。现在我们来看一个较为简单的、将风险度量的缩放应用到线性化损失分布中的问题：

下面的例子给出了特殊情况下，一个较为简单的缩放规则，我们将其称为时间平方根缩放规则。

例2.3.1（时间平方根缩放）　假设风险因子变化向量是独立同分布的，分布为Nd（0，Σ）。则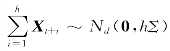，且（2.3.3）式中的分布（无论是条件的还是非条件的）满足。由（2.1.9）及（2.2.8）式，再根据时间的平方根即可得到该分布分位数和预期亏损的缩放值。如用表示预期亏损，则有(www.xing528.com)

其中σ2=b′tΣbt。显然，，且运用类似的符号，我们可以得到有。

该缩放规则在实际中经常用到，且在方差—协方差方法中很容易实施。然而，一般情况下风险因子变化的实际数据往往既不满足高斯分布的假设也不满足独立同分布的假设。在实证金融中，尽管金融风险因子的变化序列之间具有很低的相关性，但它们的波动率是变化的，这与独立同分布的模型是不一致的。为了对风险因子变化的数据建立合适模型，我们需要利用动态时间序列模型，如GARCH族的相关模型。然而，对这些模型下的风险度量如何缩放的问题知之甚少。若考虑h期损失（或其线性形式）的分布，则将风险度量的缩放应用到该分布中还依赖于我们考虑的是无条件分布还是给定条件下的条件分布。尽管几乎没有现存的理论可以对上述任何一个问题进行解释，但实证研究表明真正的缩放规则与时间平方根缩放是很不一样的。

我们可以利用蒙特卡罗法来选择h期损失分布的风险度量。假设有一个风险因子变化的模型，这个模型在非条件分析中为分布模型，条件分析中为动态模型。

在动态模型中，我们对过程的未来路径进行模拟，其中，m是一个事先确定的表示重复次数的较大值。（在非条件情况下，只需要对某个多元分布进行简单的模拟。）再将这些模拟数据代入h期损失算子中，得到基于蒙特卡罗法的模拟损失数据为：

与前面章节中介绍的一样，我们可以利用这些模拟的损失数据对损失分布及相关的风险度量进行统计推断。