混业经营金融风险映射实例

现在我们用市场风险和信用风险中的一些例子来说明前几节的内容是如何应用于一些典型的风险管理问题的。

例2.1.1（股票交易组合）　现考虑一个包含d只股票的固定投资组合，用λi来表示在t时刻股票i的股份数量。股票i的价格过程用（St，i）t∈ℕ表示。按照标准惯例在金融和风险管理中我们用对数价格，即Zt，i：=ln St，i，1≤i≤d作为风险因子。则交易组合中风险因子的变化Xt+1，i=ln St+1，i-ln St，i就与组合中股票的对数收益率相关。由此可得Vt=，故有

线性化损失则可表示为

其中，权重ωt，i：=（λiSt，i）/Vt表示在t时刻股票i的投资比例。与之对应的线性化损失算子可表示为。在给定风险因子变化分布的均值向量和协方差矩阵后，我们可以很容易计算出线性损失LΔ分布的一阶和二阶矩。若随机向量X分布的期望为μ，协方差矩阵为Σ，运用随机向量线性组合均值和方差计算的普遍规则，可以很快得到

代入风险因子变化条件分布FXt+1｜Ft的均值向量μt和协方差矩阵Σt，就可以由上式得到条件损失分布的前两阶矩。代入风险因子变化非条件分布FX的期望向量μ和协方差矩阵Σ，就可以由上式得到非条件损失分布的前两阶矩。

例2.1.2（欧式看涨期权）　现在我们考虑衍生证券交易组合的一个简单例子，该衍生证券为以无股息股票S为基础资产的、期限为T、执行价格为K的标准欧式看涨期权。我们用Black-Scholes期权定价公式来对我们的交易组合进行定价。定义函数CBS如下：

其中Φ表示标准正态分布函数，r表示连续复利无风险利率，σ表示标的股票的年化波动率，而

遵照市场公约，CBS定义中的时间是以年为单位，正好与备注2.1.2中一致。但我们关心的是日损失，所以设Δ=1/250。

该交易组合一个很显然的风险因子就是标的股票的对数价格。在Black-Scholes期权定价模型中我们假设利率和波动率均为常量，然而在真正的市场当中利率和隐含波动率都是时刻变化的，所以从业者通常用它作为波动率参数输入使用。因此我们用Zt=（ln St，rt，σt）′来表示风险因子向量。根据Black-Scholes公式，第t天的看涨期权的价值为Vt=CBS（tΔ，St；rt；σt，K，T）。风险因子变化可表示为

Xt+1=（ln St+1-ln St，rt+1-rt，σt+1-σt），

因此线性化损失可表示为

其中下标表示偏导数。Black-Scholes期权定价函数中的各导数通常被称为风险希腊值：（关于股票价格S的偏导数）称作期权的delta值；（关于时间s的偏导数）称作期权的theta值；（关于利率r的偏导数）称作期权的rho值；（关于波动率σ的偏导数）称作期权的vega值。这些希腊字母在金融衍生品交易组合的风险管理中起到了重要的作用。

例2.1.3（债券组合）　接下来我们来考虑一个由d个期限为Ti，价格为p（s，Ti），1≤i≤d的无风险零息债券组成的交易组合（同样这里时间以年为单位，因此适用于备注2.1.2）。我们用λi表示期限为Ti的债券的数量。虽然期限较长的零息债券在实际中相对比较罕见，但是由于许多固定收益证券例如附息债券或者标准互换可以看作是零息债券，因此本例仍具有重要的指导作用。

我们在现代利率理论中遵循标准公约将债券的面值p（T，T）标准化为1。零利率债券的连续复利收益可定义为y（s，T）：=-（1/（Ts））ln p（s，T），故下式成立

p（s，T）=exp（-（T-s）y（s，T））.

映射T→y（s，T）被称作是s时刻的连续复利收益曲线。在对于债券交易组合价值变化更详细的分析中我们把所有收益y（s，Ti），1≤i≤d都当作是风险因子。这样s时刻的交易组合价值可以表示为V（s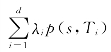）=，并且结合映射（2.2）有

通过这个式子我们就可以很容易计算出损失Lt+1的值。对它求导并运用前面线性化损失的定义同样可以得到

其中，风险因子变化为Xt+1，i=y（（t+1）Δ，Ti）-y（tΔ，Ti）。

这个公式与经典的久期概念很接近。假设收益曲线是平的，也就是y（s，T）=y（s）与T无关，并且利率唯一可能的变化就是收益曲线的平行移动，也就是对于所有的T都有y（s+Δ，T）=y（s）+δ。这些假设显然不切实际，但经常应用于实践当中。由此也可以写成(www.xing528.com)

其中

是交易组合中不同现金流到期时间的加权和，权重是与现金流的折现值成正比的。D通常被称为债券交易组合的久期。久期是传统债券交易组合和资产负债管理中的一个重要工具。这种基于久期的、用来处理债券交易组合利率风险的标准策略被称为免疫策略。在该策略下，手握一定数量的资金准备投资于不同债券且确定在未来需要支付一定已知数量资产的资产经理会以特定的方式将手上的资金投入到不同的债券中去，这种特定的方式就是令所有债券投资和负债组成的投资组合的久期等于零。根据前面的分析可知，久期衡量的是交易组合的价值对于收益曲线平行移动的敏感性。因此，久期为零意味着交易组合的头寸对收益曲线这种类型的变化是免疫的。但是，该交易组合依然可能受到收益曲线其他类型变化的影响。

若考虑具有确定收入证券的较大交易组合，如主流银行所有具有固定收入头寸的总和，此时选择交易组合中每只债券的收益作为风险因子就变得不现实了：有太多的风险因子，使得最终不可能估计出风险因子变化的分布。为了克服这个问题，人们以国家为单位选出一些基准收益率，并运用特定的程序步骤将不同基准点之间时间段内的现金流映射到相邻两个基准点上。

例2.1.4（远期货币）　现在我们考虑在远期货币中的一个多头映射。远期货币或者远期外汇是指双方约定在未来某个时间点T＞s以预先设定的汇率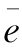买进（卖出）预先设定数量V的外汇。我们称未来的买家是合同中持有多头的一方，另一方为持有空头的一方。

我们利用以下事实来建立头寸之间的关系，那就是远期中的一个多头等价于外国零息债券的一个多头和本国零息债券的一个空头。为了更好地解释这一点，我们假设一个欧元投资者持有基于美元/欧元汇率远期货币的一个多头，持有量为V。用pf（s，T）表示一个美国（外国）零息债券的美元价格，pd（s，T）表示对应的欧元（本国）零息债券价格。欧元与美元的即期汇率用e（s）表示。则在T时刻由数量为的外国零息债券和数量为的本国零息债券组成的一个交易组合的欧元价值为VT，这显然与远期合约中多头的收益相等。

下面对美国零息债券中的头寸进行探讨。显然，这里可以选择对数汇率取及美国零息债券的收益作为风险因子，即Zt=（ln et，yf（tΔ，T））′。因此外国债券头寸的价值就等于

由此可得

其中Xt+1通常代表风险因子变化。

例2.1.5（高风险贷款的固定投资组合）　本例来自于信用风险管理领域，在这里我们将要讨论如何将整体框架应用于贷款交易组合中。贷款交易组合通常包含很多风险，其中最重要的就是违约风险，即合同的一方无法偿还其贷款的风险；利率风险，即由于利率上涨导致投资组合未来现金流的当前价值贬值的风险；由信贷息差上涨而导致损失的风险。

我们考虑一个m方的贷款组合。第i方的仓位大小为ei。遵循信用风险管理的标准惯例，风险管理时间范围Δ设为一年，这样就不需要区分两个时间尺度了（如t和s）。为了简化问题我们假设所有贷款都在同一日T＞t付清并且在T日之前没有任何付款。我们引入一个随机变量Yt，i表示t日第i方的违约状态。如果第i方在时间段［0，t］内违约则令Yt，i=1，否则Yt，i=0。同样为了简化问题我们假设回收率为零，即假设若第i个债务人违约则其对应的整个仓位ei就都没了。

对一个有风险的贷款进行估价时，我们必须得考虑违约的概率。通常，我们通过将现金流ei按照比无违约零息债券收益率y（t，T）更高的利率进行贴现来完成。更确切地说，我们对这样的贷款在t时刻的价值建立如下的模型

exp（-（T-t）（y（t，T）+ci（t，T）））ei，

其中，ci（t，T）表示第i家公司关于到期日T的信用利差。为了简化问题，我们忽略信用质量的变化并假设对于所有的i都有ci（t，T）=c（t，T）。基于以上所有的简化假设，贷款交易组合在t时刻的价值等于

由此，就可以比较容易得到下列（m+2）维随机向量组成的风险因子的Lt+1和l［t］的值了。

由于默认指标的离散性且时间范围较长，在信用风险管理中，线性化损失的重要性很小。显然，由上述两个式子可以看出，在对贷款交易组合的损失分布进行建模的过程中，主要困难在于为违约指标Yt+1，i，1≤i≤m的联合分布找到一个合适的模型。

本节介绍的风险管理框架是Risk Metrics公司所用模型的一种程式化版本。该公司将之前的成果汇总成了Risk Metrics技术文档（J.P.摩根，1996）。Mina和Xiao（2001）在更新汇总中也讨论了一些学术层面上近期的发展。在Jorion（2001）和Dowd（1998）的著作中也讨论了关于头寸的映射问题。Mc Neil和Frey（2000年）在他们的著作中重点讨论了条件风险管理与非条件风险管理的区别。

尽管从理论上来说，基于久期的套保并不令人满意，但在从业人员中依然广受欢迎。如果读者需要了解更多关于久期以及其在利率风险管理中运用的知识，我们给读者推荐一些标准金融学的教材，例如Jarrow和Turnbull（1999）的教材或者是Hull（1997）的教材。

在Duffie和Pan（1997）以及Rouvinez（1997）（Duffie和Pan（2001）中也有提及）的著作中，对衍生品交易组合的一阶和二阶近似值（即所谓的delta-gamma近似）的求解进行了介绍。