自组织演化过程——世界遗产地协同运营机制研究

（1）系统的涨落

协同学认为，涨落是系统演化的原始动力来源，没有随机涨落，就没有系统的发展。涨落可以看作是对系统稳定状态的偏离，或是系统同一发展演化过程之中的差异。但无论如何界定，涨落终究是对于系统平衡状态的破坏，是一种非平衡性。自组织理论认为，系统可通过涨落达到有序，即非平衡在一定条件下可以通过涨落被放大，通常的微涨落被放大成为巨涨落，系统实现从无序到有序从低级有序到高级有序的转变[158]。

由于非线性机制的存在，当无形资产运营体系内部出现随机事件时，比如相关者数量的增减、运营方案的变换、新的市场机遇的出现等，可通过非线性机制对这些事件进行判别选择，对于那些有利于体系发展的可以被放大，以加快体系的良性演变。无形资产协同运营机制正是这样一类非线性机制，当系统的涨落对原有体系带来的冲击低于临界状态，系统原本的结构在涨落回归的作用下得到强化；反之，如果系统涨落突破了临界状态，无形资产运营体系就会失去原有的稳定结构，而出现结构的跳跃性。跳跃性会给整个运营体系的发展带来不确定性，只有通过协同运营机制等非线性机制的关联放大作用，在得到所有子系统响应的情况形成巨涨落，运营体系才能被引导推动进入一个更稳定更有序的新状态。

（2）序参量的产生

协同学中把系统的有序或高级有序的方式称为“自组织”，把影响系统有序的关键因素称为序参量，非关键因素称为控制参量。序参量支配着各个子系统的行为，又为各个子系统所支持，它们之间的协同作用通过各子系统的相互作用表现出来，从而影响和决定整个系统自组织的程度和方向，进而决定系统的有序程度。序参量不仅是系统内部子系统集体运动（相争和协同）的产物，更重要的是，序参量在形成之后能起到支配或役使系统的作用，并主宰着整个系统的演化过程和方向。[159]

当无形资产运营体系的涨落突破临界状态时，体系就会失去原有的稳定结构，在协同运营机制等非线性机制的关联放大作用下，运营体系被引导推动进入一个更稳定更有序的新状态。在这一过程中，无形资产运营体系中各个相关者都有着自己的利益追求，他们之间既有合作又有竞争，相关者之间的竞争关系是系统演化最有力的催化剂，这种关系能够优化体系中的资源配置和整体运行的效率。同时，相关者围绕着无形资产运营形成的合作关系又是运营体系存在的前提。因此，在无形资产运营体系中，随着各方对合作与竞争关系认识的不断加深，利益相关者会逐步明确自己的定位，相互之间不断适应最终形成协调同步的运作准则，实现整个体系的协同。这一准则就是系统序参量，它会在系统的运行过程中支配着所有成员的行动，约束并影响着无形资产运营体系中的利益分配原则、信息共享程度、成员信任程度等群体行为，支配着体系演化发展的方向。

（3）协同状态的形成

协同学的稳定性原理认为，序参量对系统的自组织演变过程起着决定性作用，而控制参量是通过影响序参量来实现对系统的影响的。当外部控制参量发生变化时，系统所处环境以及系统自身结构失去了稳定性，继而新的系统结构出现，但控制参量的变化不会停止，新结构的产生、存在和运行不会停留在稳定状态，随着控制参量的继续变化，系统会不断向着更新更稳定的状态发展演化。由此可以看出，系统的自组织过程本质上就是稳定性与不稳定性的统一。这一过程可以通过图7-2来描述。

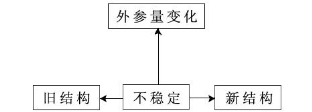
图7-2　协同状态的形成

根据协同学原理，自组织演化过程模型通过下述三个步骤来描述协同状态的形成。

（1）通过线性稳定性分析求解非线性方程的非稳定解，寻找无形资产运营体系可能存在的失稳点，包括稳定性丧失的范围、时间和条件。无形资产运营体系的演化可以通过如下模型[156]进行描述。

设：

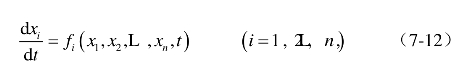
其中，x1，x2，LLxn是n个说明无形资产运营体系状态的变量。在无序的稳定热力学分支上，它们均为零，可以表示为：

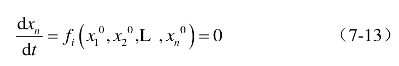
现假定方程具有定态解{Xio}，与定态解有微小偏差解{Xi}可以写成线性形式，即：(www.xing528.com)

对方程进行泰勒级数展开并只取线性项得：

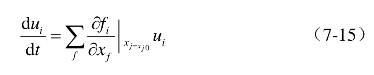
求解该方程的结果为，a∂是方程对应的根，若a∂皆为负，态解{Xio}是稳定的，若a∂中有一个为正，表示{Xio}是不稳定的，该不稳定解即为无形资产运营体系的失稳点。

（2）无形资产运营体系在失稳之后，通过协同理论来找寻系统状态变量之间的关系，即需要应用充分体现自组织过程的支配原理，用绝热消去方程来找寻慢变量。用u来表示系统的慢变量，s表示快变量，建立如下的微分方程组：

假定变量u和s的阻尼系数：α＞0，β＞0，忽略上式中非线性项us和u2，即得到两个非耦合方程，因为s代表稳定模，u代表不稳定模，因此从数学上表示把s表示成u的函数，即可说明u支配s，s伺服于u，消去式（7-16）中的s，得：

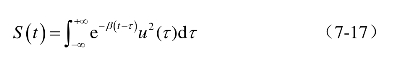
使用分部积分法，得：

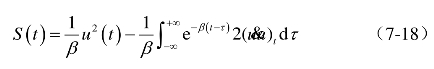
u是慢变量，可把u&看作一个小量，根据绝热近似思想，只要成立，即可忽略上式中的积分项，得：

把时刻t的s变成同一时刻t的u函数，即说明u支配s。上面只是列举了两个变量的情况，实际情况要复杂得多，如果是很多变量的情况下，则需要使用绝热消去原理直到最后的结果。第三步建立和求解序参量方程。把式（7-19）带入（7-17），得到序参量的方程：

求解方程即得到u在相变过程中随时间变化的规律。在无形资产运营体系中，该序参量u就是运营体系的运作准则，它支配着整个体系向更高级、更有序的结构演化，并使运营体系最终实现协同，包括功能协同、目标协同、时间序列协同和体系结构协同，从而提高运行效率，降低构成部分之间的摩擦，减少损耗，避免冲突，提高系统应变能力，从而使得世界遗产地无形资产运营体系实现协同一致。

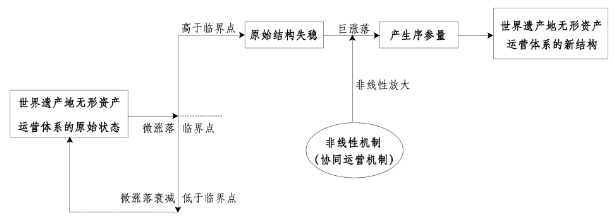
图7-3　无形资产运营体系自组织演化过程协同状态的形成