世界遗产地无形资产协同运营机制分析

由于遗产管理机构所具有的事业部门的性质，以及无形资产运营对专业知识和相关经验的需要，在世界遗产管理权与经营权分离呼声越来越高的大背景下，由专业的无形资产运营企业在政府部门和遗产管理机构的监督下对世界遗产地的无形资产进行开发经营将是大势所趋。在这一层委托代理关系中，遗产管理机构作为政府的代表来执行世界遗产管理的职能，其任务是在实现世界遗产地有效保护的前提下，通过合理开发使得社会公众能更好地享用遗产资源的各种价值；而无形资产运营企业参与其中的目的就是实现利益最大化。

在博弈的第一阶段，遗产管理机构可以选择委托企业进行无形资产的运营，也可以选择不委托，采用自主管理或联合管理的模式进行开发；在遗产管理机构选择委托的情况下，博弈第二阶段中代理人公司可以根据其预期收益选择接受或不接受委托；代理人在选择接受委托的情况下，他还可以在第三阶段选择是努力执行契约内容，还是消极偷懒，即按照自身利益最大化的原则来运营遗产地无形资产。

在第一阶段，假设遗产管理机构判断无形资产运营企业会选择努力，那么根据模型中的假设，委托人的期望得益为

因此，对于风险中性的管理机构来说，当Pt×[R1-W （R1）]+（1-Pt）×[R2-W （R2）]＞0时，就会选择委托而放弃其他运营模式。这就是遗产管理机构选择委托的基本条件。

第二阶段，只要代理人企业接受委托负责无形资产运营的期望收益大于不接受时的收益，那么企业就会选择接受委托。企业与遗产管理机构委托代理的参与约束，即：

第三阶段，若代理企业选择努力，则根据委托人的要求开发和经营无形资产的期望得益为：

若企业选择偷懒，则按照自身利益最大化的原则运营无形资产的期望得益为：

只要代理人企业按照和遗产管理机构的契约约定的期望得益大于违背契约时的期望得益，即：

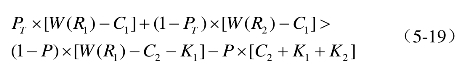
那么，代理人企业就会选择努力遵守契约。上式也就是世界遗产管理机构与无形资产运营企业委托代理关系的激励相容约束。

为了更有针对性地制定代理人的激励政策，现只考虑代理人企业的努力程度对博弈结果的影响。假设代理人企业在无形资产运营的过程中可选择的努力水平e分布于一个连续区间，其产出R是一个随机函数R =R（ e）=2e +η，其中η是均值为0的随机干扰项。代理人企业在代理无形资产运营过程中的负效用（即精力以及经济方面的消耗）是努力水平的单调递增的凸函数C =C （e） =e2。现假设代理人企业有正值的机会成本U，则只有在接受委托时的期望收益不小于U，即W ×[R（ e）-C （e）]≥U时，代理人公司才会接受委托，所以上式即为参与约束。

从参与约束来看，在代理人公司接受委托的情况下，遗产管理机构必然希望支付的代理成本越少越好，这就使得实际的参与约束为W ×R（ e）=U +C （e），这样委托人的收益函数为：

由双方的收益函数可知，遗产管理机构首先可以解出符合自身利益的代理人企业努力水平1e，如图5-3所示。

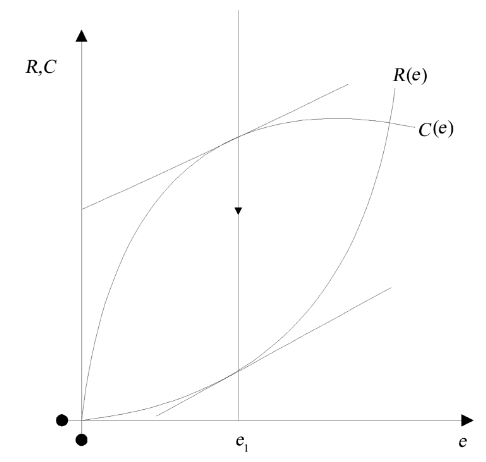
图5-3　遗产管理机构希望代理人企业的努力水平（满足参与约束）

图中，R（e）为凹函数，C（e）为单调递增的凸函数，e1即能够使得R（e）与U+C （e）的切线相平行的努力水平。假使e＜e1，则说明代理人企业在代理过程中有偷懒行为；假使e？e1，则说明代理人公司在接受委托后是按照遗产管理机构的要求执行契约的。(www.xing528.com)

但是，在满足参与约束的情况下，有可能代理人公司愿意接受委托但努力水平不是e1，因为其根本目标是追求利益的最大化，因此，只有当e1能实现其最大利益时，代理人公司才会自觉选择e1，即有：

上式即为模型的激励相容约束。满足此约束条件就意味着当代理人企业的利益与遗产管理机构的利益完全一致时，其就会符合委托人的最大利益。如果遗产管理机构按照上述激励相容约束和参与约束来设计报酬函数，就能使代理人企业的行为符合自己的利益。

由于遗产管理机构无法掌握代理人实际的努力情况，因此，遗产管理机构只能根据代理人企业运营无形资产的实际结果支付报酬。假设遗产管理机构支付代理人企业报酬的计算公式为：

其中M、N均为常参数。此外，遗产管理机构在委托代理关系中还要承担以契约形式委托的签约成本、不对称的高信息成本、资产专用性成本以及不确定性风险成本，总计为交易成本T。

由此可以得出委托代理双方各自的收益函数，遗产管理机构的收益函数为：

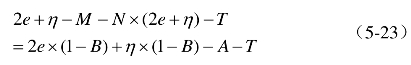
由于η是均值为0的随机干扰项，上式右侧可整理为：

代理人企业的收益函数为：

期望收益即为M+2N ×e -e2。

在此假设下，参与约束为：

由此，在代理人企业的选择方面，假如遗产管理机构是风险中性的，则期望净利益M+2N ×e≥1+e2时，代理人企业就会选择接受委托。代理人企业的期望收益为M +N×（2e+η）-e2。当代理人企业是风险中性时，e1=N即符合代理人企业的最大利益，也就是符合其利益的最佳努力水平取决于N。

在遗产管理机构的选择方面，首先，其选择必须满足代理人企业参与约束条件的下限：M +N×（2e+η）≥1+e2。这时遗产管理机构的收益计算公式为：M+N×（2e+η）-1-e2-T ，期望收益为：2e-e2-2，可得e2=1是符合遗产管理机构利益最大化的企业最佳努力水平。令e1=e2=1，并对约束条件M +N×（2e+η）=1+e2两边求数学期望，可得M=0，N=1。遗产管理机构的最大激励报酬的运算式为：

由以上分析可知，在动态博弈中，双方会通过自己的行动来争取对方的信任和合作，从而放弃短期利益来选择长远的整体的利益最大化。但是要调动双方遵守契约的积极性，就要建立符合世界遗产管理要求的委托代理机制以及对代理人企业的控制机制，其核心目的在于：①合理分配遗产管理机构与代理人企业的权利，寻求控制权与自主权之间的平衡点，避免世界遗产管理机构控制权过度，或代理人企业自主权过大所造成的监督不力的现象；②统一博弈双方对于世界遗产保护与开发经营之间关系的认识，避免体系内由于存在多重目标所造成的矛盾冲突，采取合理的激励手段鼓励被授权企业始终以整体利益最大化作为经营目标。