解读数学花园中的不可能问题及其重要性

科学根据现象总结出规律，就可以做出许多预见。天文学不但能告诉我们明天会不会发生日食，还能准确地预告我们2009年会发生一次金星凌日，就是金星恰好在地球和太阳之间穿过。气象学就差一些，因为连明天会不会下雨这样的问题，预报也经常弄错。

在科学发展中，更加困难的任务是准确地告诉人们，什么事情是不可能的。物理学告诉我们永动机是不可能的，化学告诉我们氩不可能氧化，数学也做出了许多不可能的结论。

怎样用加号、乘号和括号，把4个“2”写成一个得数是10的算式？你很快就会找到：2+2×（2+2）=10。要写出得数是3是不可能的。但是要做出这样的判断就难得多。第一，你得察觉出这是不可能的；第二，你要证明为什么这是不可能的，当然就难得多了。

许多有名的数学问题就是这样。

例如用一根直尺和一个圆规：

把一个已知角三等分；

作一条线段，它的长度等于一已知线段的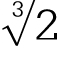倍；

作一个正方形，它的面积和一个已知的圆面积相等。

这3个作图题看起来都不难。但是，在很长的时间里，不知花了多少人的精力，总是做不出来。最后发现，这3个问题只用圆规和直尺是不可能解决的！

如果有一个人声称他解决了这3个问题中的一个，要指出他错在哪里是一件很简单的事。但是，要严格证明这3个问题是不可能的，就要用到许多高等数学的知识。

很多少年有闯禁区的胆量，敢于去做前人认为做不到的事，这是很可贵的！但是在这之前，应该大体了解一下前人为什么没有做到，如果可以做到而前人没有做到，那么，前人的漏洞和错误在哪里。这样了解是闯出新路所不可缺少的。不然就不是勇敢而是莽撞了，最后就会碰壁，白白浪费了许多精力和时间。

数学中另一个有名的问题是解方程的公式。

大家都知道一次方程ax+b=0，它的解是x=-；

二次方程ax2+bx+c=0有两个解，

三次和四次方程的解法只有300年左右的历史，它们的公式得写满一两页纸。

后来，人们用了整整一个世纪，想找到五次、六次和更高次方程式的一般解法。这就是要找到一个公式，用方程式的系数做加、减、乘、除或者开方得到方程式的解。但是都失败了。(www.xing528.com)

这时候，年仅19岁的法国青年数学家伽罗华，从前人的失败中总结出了深入的规律，他证明了五次以上的方程式，不可能用系数的加、减、乘、除或开方解出来。

为了证明这一点，伽罗华创立了一个全新的数学分支——群论。群论开创了数学的一个新时期——近代数学的时期。他以群论为工具，解决了长期困惑着数学家的问题。

伽罗华的发现是如此的深奥，以致当时最权威的数学家都不理解。他们把他的手稿保存了许多年，才弄明白他的发现是怎么一回事。

不幸的是，伽罗华把他的手稿寄出之后的第二天就被杀害了。人们为了纪念他的功绩，把许多与他有关的数学概念，用他的名字来命名，比如伽罗华理论、伽罗华群、伽罗华域。

100多年来，许多不可能问题，都是按照伽罗华开创的路线去证明的。

名师导读

马教授说“科学发展中，比预报更加困难的任务是准确地告诉人们，什么事情是不可能的……而想要下判断‘不可能’得先察觉出这是不可能的，并要证明这是不可能的。”显然，想要察觉“不可能”，就要拥有开放的头脑和大胆质疑的精神；想要证明问题就需要严密的逻辑推理能力；这两点对数学学习来说尤其重要。在小学数学学习中，我们也要重视培养小朋友们的质疑精神和逻辑推理能力。

小学数学教学中涉及到的概念、方程式、应用题等相对比较简单，在此阶段小朋友们的思维正逐渐从具体形象思维向抽象逻辑过渡，伴随着丰富的思维活动，掌握一定的逻辑思维运用方法，会让我们思考和解决问题更有方向和方法。

例1：猜数游戏。

①这个数比5大比7小？这个数是几？

②这个数是一个两位数，个位上是4，这个数比55小。从下列答案中选择，在合适的答案下打√。

例2：鸡兔同笼，有9个头，26条脚。鸡、兔各有多少只？

鸡和兔的数量不知道，只知道头数和脚数。根据鸡与兔一共有9只，假设鸡有1只，那么兔有8只，腿共有34条……在这样逐一举例中，直至寻找到所求的答案。在探索答案的过程中我们借助表格，发现“鸡兔同笼”问题中蕴含的规律，“头数不变，鸡增加1只，兔减少1只，腿减少2条”的规律。正是通过经历这样的尝试与猜测、不断调整的学习过程，我们才能发现规律，运用规律，从而解决问题。

培养逻辑推理能力不是一蹴而就的，想要成为福尔摩斯神探需要大量的学习和认真的思考！小朋友们，不要只会说“Nothing is impossible”，试试证明“What is impossible”！