DY溢出指数模型及其应用：全球金融市场变化研究

DY溢出指数模型（2012）可以测算跨市场风险溢出的方向和强度。该方法可以估算特定市场间总溢出指数、定向溢出指数以及动态溢出指数。该模型使用Cholesky因子正交分解计算简单向量自回归VAR框架下的总溢出，直观描述变量间的相互影响关系，并且按照Koop和Pesaran提出的广义向量自回归框架下的分解方法（KPSS）来规避方差分解结果对变量排序产生的依赖性。下面我们介绍相关模型。

首先构建N个变量的向量自回归模型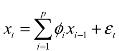：，其中εt是独立的扰动项，服从εt～E（0，ε）分布。

资产自身方差份额表示由资产xi自身的冲击所带来的对H步后xi的预测误差方差，交叉方差份额表示由其他资产xj的冲击所带来的对H步后xi的预测误差方差，也就是资产xj的方差溢出。对H步后的预测误差方差进行分解：

其中ε是误差向量εt的方差矩阵，而σij是第j个方程的标准差，ej是选择向量。

为了更好地量化和比较各溢出指数的大小，将方差分解矩阵的每个元素都标准化：

总溢出指数衡量各资产波动性冲击溢出对总预测误差防方差的贡献，表示为：(www.xing528.com)

广义冲击响应和方差分解对于变量的排序不变，使用广义方差分解矩阵的标准化元素来计算方向性溢出，资产i市场从其他资产j市场接收到的风险溢出表示为：

资产i市场传递给其他资产j市场的风险溢出表示为：

净溢出指数表示资产i对其他资产市场的风险溢出和其接收到的来自其他资产市场的风险溢出之差，表示为：

净成对波动溢出是从资产i市场传递到资产j市场的波动率冲击与从资产j市场传递到资产i市场的波动率冲击之差，用来衡量一个资产i市场对另一个资产j市场的波动的贡献，表示为：

另外，溢出指数建立在VAR模型的基础之上，在测度之前评估它所构建经济系统的平稳性以及之间的协整关系。要将变量波动率经过对数化处理后，通过平稳性检验，再进一步构建VAR模型。