新冠疫情下全球金融市场变化：隐含波动率计算

1.数据选取与描述

本章选取2015年2月9日到2020年12月30日的上证50ETF期权数据计算期权隐含波动率，其中包括合约代码、到期日、执行价格、期权价格、标的价格、期权交易量以及无风险利率，数据来源于Wind和锐思数据库。此外还利用SAS接口从锐思数据库获取了上证50ETF的5分钟高频交易数据，用于计算已实现波动率。

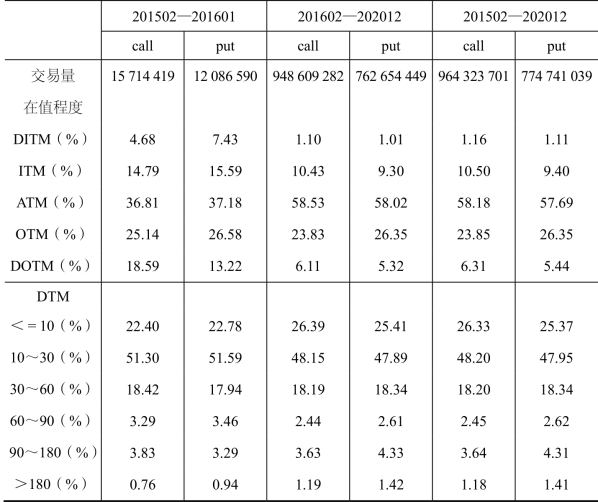
表10.1中统计了不同时间区间不同类型期权的交易情况，由于2015年A股市场发生剧烈波动，期权交易也可能与常规市场状态下不同，所以我们将其单独分类。其中我们根据在值程度（Moneyness），按照3%和10% 的分界点将期权分为平值期权（ATM）、浅度价内期权（ITM）、浅度价外期权（OTM）、深度价内期权（DITM）和深度价外期权（DOTM）。DTM为期权的剩余期限。统计显示，每个时间区间内看涨期权的成交量均大于看跌期权的成交量，投资者更倾向于交易平值期权，除2015年外平值期权的交易量均占到55%以上，这与平值期权的流动性最好的事实相符。其次浅度虚值期权的交易量较高，均超过20%。与其他年份不同，2015年深度价外期权表现较为异常，成交量占比远高于其他时间区间，这主要是市场剧烈波动导致的，因为对于想要对冲股市过度波动的投资者和投机者来说，深度价外期权更加具有吸引力。此外，从期权的剩余期限来看，接近一半的交易集中在剩余期限为10至30天的期权，每个区间段剩余期限小于30天的期权交易量占总交易量比例均超过70%，说明短期期权流动性好，杠杆率高，是投资者的交易首选。通常来说，期权交易量越大，信息含量越多，通过对上证50ETF期权交易量的特征分析，为我们在研究中进一步选择期权提供了依据。

表10.1　上证50ETF期权交易量

2.计算无模型隐含波动率

本章采用Bakshi等（2003）提出的方法来计算上证50ETF期权的无模型隐含波动率（MFIV），因为波动率合约的价值可以由虚值的看涨期权和看跌期权来表示，所以我们通过虚值的上证50ETF期权来计算隐含波动率。

在实际计算中，我们使用的是连续积分求解的方法，理论上需要对执行价格在区间（0，∞）上积分，但是每一天的期权数量较少，执行价格数量也较少，并且执行价格的上下限也与积分区间不符合，无法满足连续积分的要求。如果在此条件下进行计算，会导致较大的离散误差和截断误差。为了增加执行价格数量，满足计算要求，这里以B−S模型为映射工具，采用三次样条插值法对波动率微笑曲线进行插值处理。(www.xing528.com)

首先，选取上海银行间同业拆放利率（shibor）作为无风险利率，因为期权到期时期与官方公布的shibor利率期限不匹配，所以要对shibor进行插值，得到与期权期限对应的无风险利率。然后，根据K/S筛选出虚值期权。对于看涨期权来说，K/S＞1为虚值期权，而对于看跌期权来说，K/S＜1是虚值期权。接下来，通过B−S期权定价模型求解得到虚值期权对应的B−S隐含波动率（IV），这样就形成了执行价格和隐含波动率一一对应的关系。在（Kmin，Kmax）内使用三次样条插值法拟合隐含波动率与执行价格的函数关系，并且对（Kmin，Kmax）范围之外的部分进行水平外推，得到反映执行价格和B−S隐含波动率关系的连续曲线。接着，在区间（0.3S，3S）范围内选取1000个执行价格K的等间距点，再次利用B−S模型，将这些执行价格对应的隐含波动率带入到B−S公式中得到下一步计算无模型隐含波动率所需的虚值期权的价格。最后，将经处理后的虚值看涨期权和虚值看跌期权数据代入到BKM模型中，计算出上证50ETF期权的无模型隐含波动率MFIV。

通常在每个交易日会有四种不同到期期限的期权合约，分别是当月、下月和之后的两个季月。一般认为期权交易越活跃，其中包含的信息量越多。由上文期权交易量的分类统计可知，剩余期限为10到30天的期权合约交易量最大，所以我们剔除了剩余期限小于9天的合约后，选择距离到期日最近的期权合约计算无模型隐含波动率。此外，为了便于观察和比较，对计算出的结果进行了年化处理。上证50ETF期权无模型隐含波动率走势如图10.2所示。

图10.2　无模型隐含波动率与已实现波动率

我们根据式（1）运用上证50ETF高频交易数据计算了已实现波动率，同样对计算结果进行了年化处理。上图同时展示了隐含波动率和已实现波动率，可以看出隐含波动率与已实现波动率具有明显的一致性，在市场行情经历较大波动时，隐含波动率会上升，特别是在2015年，中国股票市场出现剧烈波动，股票价格经历了大幅度的上涨和下跌，反映在隐含波动率中，该时间段内隐含波动率异常的高。此外，在2020年初和下半年的市场波动中，隐含波动率也表现出一段时间的较高数值。由此可以看出，无模型隐含波动率能够较好地捕捉市场波动情况。

此外，我们由图10.2可以看出，国内市场价格波动较大。2015年2月9日至2020年12月30日，上证50ETF的平均已实现波动率为16.42%，50ETF期权的平均隐含波动率为23.98%。相比之下，同期美国标普500指数平均已实现波动率约为14.62%，平均波动率指数VIX约为17.49%。如果将隐含波动率与已实现波动率的差值定义为波动率溢价，那么中国市场的波动率溢价约比美国市场波动率溢价高1.6倍，这说明中国市场的波动幅度更大。

3.隐含波动率在波动率预测中的作用

本节中我们将建立前一节第一部分中节中提出的波动率预测模型。首先我们应用已实现波动率和隐含波动率对模型进行估计，并且分析各个预测模型的样本内情况，而后我们的重点是对比模型的样本外预测能力，以此来评价隐含波动率的作用。