与总体状态下的实证检验类似,在进行均值溢出实证时,首先进行不同行情下三个市场的平稳性检验,然后判定最优滞后阶数,进而进行格兰杰因果检验,再检验不同行情下市场间的协整关系,然后估计VECM模型判断短期的均值溢出效应,然后进行广义脉冲响应,判断均值溢出效应的动态效果;在进行波动溢出实证时,首先验证不同市场行情下各市场是否存在ARCH效应,然后进行单变量的GARCH效应检验,最后进行三个市场间BEKK-GARCH模型的构建,检验不同市场之间的波动溢出效应。
1.不同行情下的均值溢出实证检验
(1)ADF检验
经计算发现上涨和下跌阶段,指数、期货、期权市场在1%的显著性水平下均接受存在单位根的零假设,说明价格序列是非平稳的,收益率序列均拒绝存在单位根的零假设,说明收益率序列是平稳的。所以上涨和下跌的市场行情下,上证50指数、期货、期权的价格时间序列都是一阶单整的,即序列满足I(1)。
表7.10 不同市场行情下指数、期权、期货的价格和收益率ADF检验

(2)最优滞后阶数
经计算在下跌的市场行情下,共有3种准则支持滞后阶数为8的结果,数量最多,因此下跌阶段的最优滞后阶数为8;在上涨的市场行情下,共有3种准则支持滞后阶数为7的结果,数量最多,因此上涨阶段的最优滞后阶数为7。
(3)格兰杰因果检验
如表7.11所示,在下跌的市场行情中,各格兰杰因果检验均拒绝了原假设,表明指数、期权、期货的价格时间序列两两之间均存在双向的格兰杰因果关系,不同市场之间可以相互引导。从F统计量的大小关系来看,期权、期货、指数的引导能力是依次递减的。
表7.11 不同市场行情下格兰杰因果检验
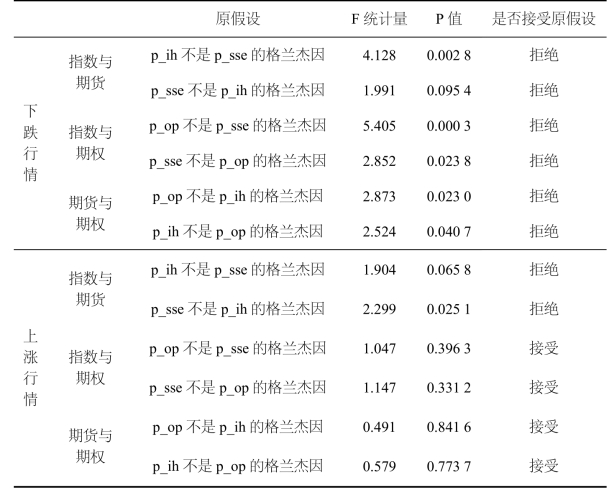
在上涨的市场行情下,只有指数和期货之间存在双向的格兰杰因果关系,并且指数的引导能力大于期货;期权与期货之间、期权与指数之间均不存在格兰杰因果关系。
(4)协整检验
在下跌和上涨的市场行情下,指数、期权、期货对数价格时间序列在1% 显著性水平下拒绝了协整秩为零的原假设,接受了协整秩至多为1的原假设,说明三个变量之间存在1个不相关的协整向量,协整秩为1,三者市场之间具有共同的长期趋势。
表7.12 不同市场行情下协整检验(迹检验)

(5)VECM模型
短期调整关系。下跌的市场行情下,从α可以看出矩阵指数、期货、期权对应的短期调整系数均不显著,说明当期货、期权、指数的长期均衡关系出现偏差时在短期很难得到调整。从矩阵Γ可以看出,上证50指数、上证50股指期货和上证50ETF期权在市场行情下跌的时候具有双向均值溢出效应,但是与总体市场行情下差别显著。指数收益率受到指数收益滞后1期、2期的影响,受到期货滞后2期的影响,受到期权滞后1期的影响;期货收益率受到指数收益率滞后1期、2期的影响,受到期货本身滞后2期的影响,受到期权滞后1期、3期的影响;期权收益率受到指数滞后1期、2期的影响,受到期货滞后3期的影响,受到期权本身滞后3期的影响。因此三个市场间的领先滞后关系为期权领先于期货,期货领先于指数。
上涨的市场行情下,α矩阵的系数均显著不为零,说明当指数、期货、期权的长期均衡关系出现偏差时,短期的调整效果显著。从矩阵Γ可以看出,指数收益受到本身滞后1、2、5、6期的影响,受到期货滞后5期、6期的影响,不受期权的影响;期货受到指数滞后1期、6期的影响,受到期货本身滞后5期、6期的影响,没有受到期权的影响;期权受到指数滞后1期、5期、6期的影响,受到期货滞后5期、6期的影响,受到期权本身滞后3期、4期的影响。与总体行情和下跌行情相比,期权价格变动相对滞后,且均值溢出效应较弱。因此三个市场的领先滞后关系为指数领先于期货,期货领先于期权。
表7.13 不同市场行情下误差修正模型系数检验

续表

协整关系检验。由表7.14所示,下跌行情下的误差修正项为:
![]()
![]()
上涨行情下的误差修正项为:

表7.14 不同市场行情下协整方程检验

稳定性检验。由图7.5所示,不论是上涨行情还是下跌行情,经过单位圆检验,除了VECM模型本身所假设的单位圆之外,不存在大于1的根,因此两个模型都是稳定的。(https://www.xing528.com)

图7.5 不同市场行情下VECM模型单位根检验
(6)广义脉冲响应
在下跌的行情中,面对来自不同市场冲击的影响,股指、期货、期权在第一期均受到自身的影响最大,第二期均受到期货的影响最大,4期开始均受到自身影响最大。与总体样本相比,下跌的行情中,市场对于冲击的反应程度相对较大。
在上涨的市场行情中,不同市场受到冲击,都是先增大后减少的过程,并且在整个过程中受到本身的影响是最大的。与总体样本区间相比,市场对于冲击的反应程度相对较小。

图7.6 不同市场行情下广义脉冲响应
2.不同行情下的波动溢出实证检验
(1)ARCH效应
与总体情况下的实证检验类似,首先进行ARCH效应检验,判断是否能够建立后续的GARCH模型,然后进行GARCH(1,1)建模,最后进行BEKK-GARCH的分析,检验指数、期货、期权市场间的波动溢出效应。
首先,设定指数、期货、期权的指数收益率模型,并利用最小二乘法进行估计,下跌行情下的结果为:
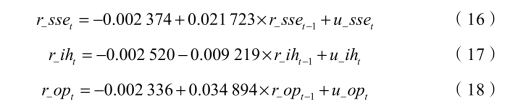
上涨行情下的结果为:

分别对不同行情下的指数、期货、期权的收益率模型进行条件异方差的ARCH-LM检验,如表7.15所示,在上涨和下跌的市场行情下,指数、期货、期权收益均能拒绝原假设,收益率数据存在ARCH效应,数据可以进行后续的BEKK-GARCH模型构建。
表7.15 不同市场行情下的ARCH效应检验

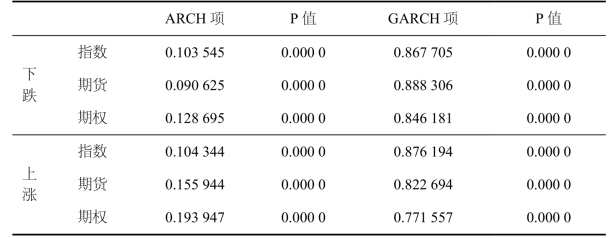
(2)单变量GARCH模型
通过对不同行情下的指数、期货、期权的收益率建立单变量GARCH(1,1),检验不同市场的波动性特征,得出的结果如表7.16所示。
三个市场的ARCH项系数和GARCH项系数均通过了1%显著性检验。GARCH项系数均远大于ARCH项系数,表明三个市场均受到条件方差的影响更大,两系数之和接近1,满足GARCH模型的稳定性条件,且市场信息对波动性的影响具有很大的持续性。
但是受影响来源和程度不同,不同市场在不同的行情下表现出较大差异。下跌阶段,三个市场的ARCH项均较小,GARCH项均较大,说明下跌阶段受到新信息的影响更大,受到条件方差的影响更小。而在下跌阶段,期货受到新信息的影响最大,而在上涨阶段期权受到新信息的影响最大。不同市场在不同的行情下表现出较大差异。
表7.16 不同市场行情下单变量GARCH模型参数
(3)BEKK-GARCH检验
从表7.17可以看出,在下跌的市场行情下,指数、期货和期权的波动均受到自身的影响,其中期货和期权的GARCH项和ARCH项均显著不为零,因此条件方差受到历史条件方差和随机扰动的影响,但是指数仅GARCH项显著不为零,因此指数波动仅受到历史条件方差的影响。在上涨的市场行情下,期货和指数波动受到自身历史条件方差和随机扰动的影响,但是期权波动仅受到历史随机误差的影响。
从交叉项可以看出,在下跌的市场行情下,指数受到期货和期权条件方差和历史随机扰动的影响,因此期货和期权均对指数有显著的波动溢出效应,而期权仅受到指数历史随机扰动的影响,期货仅受到指数历史条件方差的影响,指数虽然对期货和期权能够产生溢出效应,但溢出效应仅仅通过历史波动或者历史随机扰动产生,因此指数对期货和期权的波动溢出效应较小;期货和期权之间同样存在双向波动溢出效应,但是期权仅受到期货随机扰动的影响,但从系数绝对值大小来看,期权和期货之间的波动溢出效应孰强孰弱无法判断。在上涨的市场行情下,指数均受到期权和期货条件方差的影响,但是没有受到历史随机扰动的影响,而期权和期货市场均受到指数历史方差和随机扰动的影响,期权受到期货随机扰动的影响,期货受到期权历史方差的影响,因此三个市场之间存在双向波动溢出效应,但是溢出效应的大小无法通过系数绝对值得出明确结论。
因此,在不同的市场行情下,指数、期货、期权三个市场均存在显著的双向波动溢出效应,行情不同,波动溢出效应差异较大。在下跌的市场行情下,期货和期权的溢出效应明显大于指数的溢出效应。在上涨的市场行情下,三者之间溢出效应大小无法判断。
表7.17 不同市场行情下BEKK-GARCH模型实证

续表

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




