1.ARCH效应检验
根据上文对数收益率的图形和描述性统计,发现指数、期货和期权三个市场的时间序列存在较为明显的波形聚集现象,这一特征表明这三个市场的收益率时间序列有很大可能存在自回归条件异方差。因此首先需要对序列进行ARCH效应检验,若存在条件异方差,则可以进一步建立GARCH模型,判断三个市场间的波动性特征。
首先,分别设定指数、期货、期权的指数收益率模型:
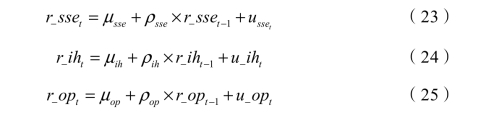
利用最小二乘法进行估计,得出结果如下:

分别对指数、期货、期权收益率的收益率模型进行条件异方差的ARCH-LM检验,如表7.25所示,对上证50指数、期货、期权的收益率序列进行ARCH效应检验,F统计量和N×R2统计量的P值均小于10%,表示在10%的显著性水评下拒绝序列不存在ARCH效应的原假设,说明三个市场的收益率序列均存在ARCH效应,数据可以进行后续的BEKK-GARCH模型构建。
表7.25 ARCH效应检验

2.单变量GARCH模型检验
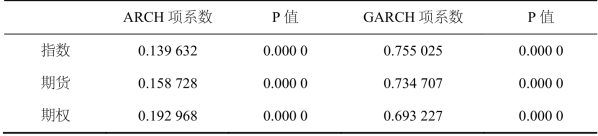
通过分别对指数、期货、期权的收益率建立单变量GARCH(1,1),检验不同市场的波动性特征,各模型参数的估计结果如下表所示,其中α和β分别代表ARCH项系数和GARCH项系数,分别表示市场受到新信息冲击和往期信息的影响程度,α+β代表受到市场整体信息的影响程度,代表了波动的持续性。(https://www.xing528.com)
如表7.26所示,三个市场的ARCH项系数和GARCH项系数均通过了1%显著性检验。GARCH项系数均远大于ARCH项系数,表明三个市场均受到往期信息的影响更大,两系数之和接近1,满足GARCH模型的稳定性条件,且市场信息对波动性的影响具有很大的持续性。三个市场对比来看,指数的GARCH项系数最大,ARCH项系数最小,说明指数虽然受到新信息的影响最小,受到往期信息的影响更大,相比之下,期权受到新信息的影响最大,受到往期信息的影响最小。
表7.26 单变量GARCH模型参数
3.BEKK-GARCH模型
表7.27反映了疫情下上证50指数、上证50股指期货和上证50ETF期权的波动溢出效应系数,从aii和bii可以判断各市场受到自身变化的影响,指数、期货和期权的ARCH项系数均显著不为零,因此三者均受到自身历史随机扰动的影响,而指数和期权的GARCH项系数均显著不为零,期货的GARCH项系数不能拒绝原假设,说明仅指数和期权均受到自身历史条件方差的影响,期货不受自身历史条件方差的影响。
从交叉项来看,指数与期货之间存在显著的双向波动溢出效应,但是指数仅受到期货历史条件方差的影响,期货仅受到指数历史随机扰动的影响;指数与期权之间存在显著的双向波动溢出效应,但是指数受期权的历史随机扰动和历史条件的方差的影响,期权仅受到指数历史条件方差的影响,因此期权对指数的波动溢出效应大于指数对期权的波动溢出效应;期货与期权之间存在显著的双向波动溢出效应,但是期权仅受到期货历史随机扰动的影响,期货仅受到期权历史随机扰动的影响。
总体而言,疫情期间,上证50指数、上证50股指期货和上证50ETF期权波动性均受到自身扰动的影响,同时也受到其他两个市场波动溢出效应的影响,期权与指数相比波动溢出效应更大,但是期货与期权、期货与指数相比波动溢出效应大小无法判断。
表7.27 BEKK-GARCH模型

续表

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




