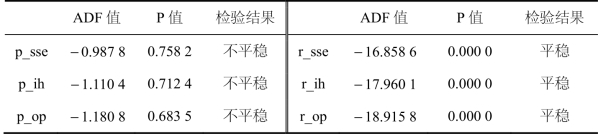
建立向量误差修正模型需要满足时间序列平稳的要求,从而保证回归结果的准确性,因此,首先利用ADF进行平稳性检验。由表7.19可知,在不同的显著性水平下,指数、期权、期货的价格序列的ADF统计量均大于临界值,接受存在单位根的零假设,说明价格序列是非平稳的;而在不同的显著性水平下,三者的收益率序列均小于临界值,拒绝存在单位根的零假设,收益率序列是平稳的。从平稳性检验结果来看,指数、期货、期权的价格时间序列是一阶单整的,即满足I(1)。
表7.19 上证指数、期权、期货的价格和收益率ADF检验
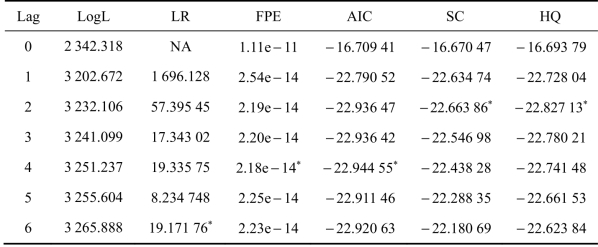
在建立向量误差修正模型之前首先需要选择最佳的滞后阶数,根据表7.20,有SC和HQ两种准则支持滞后阶数为2的结果,而FPE和AIC支持滞后阶数为4的结果,由于本章利用VECM模型进行分析,滞后两阶过于简洁,无法准确显示更高滞后阶数的结果,因此本章选择的最优滞后阶数为4。
表7.20 VECM模型最优滞后阶数选择
通过格兰杰因果检验可以检测不同变量之间的相关关系,表明一个变量对另一个变量的预测能力,为VECM模型的理论结果提供有力支撑。如表7.21所示,指数与期货的格兰杰因果关系检验中,接受期货不是指数的格兰杰因的原假设,拒绝指数不是期货的格兰杰因的原假设,因此期数引导期货;同理,由指数与期权的格兰杰因果关系可以看出指数引导期权,由期货与期权的格兰杰因果关系可以看出,期货引导期权。因此指数、期货、期权的引导关系为指数→期货→期权。
表7.21 格兰杰因果检验

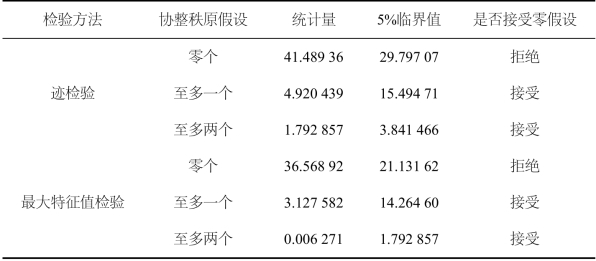
由于各时间序列之间存在协整关系时VECM模型成立的前提,因此本章在利用Johansen的MLE方法估计上文建立的VECM模型之前,先对各时间序列进行协整检验,如表7.22所示,迹检验和最大特征值检验的结果均表明指数、期权、期货对数价格时间序列在5% 显著性水平下拒绝了协整秩为零的原假设,接受了协整秩至多为1、协整秩至多为2的原假设,说明三个变量之间存在1个不相关的协整向量,协整秩为1,三者能够保持协整关系。
表7.22 协整检验
下面对上证50指数、期权、期货进行VECM建模,滞后期为4,协整秩为1,选择包括常数项不包括时间趋势的形式:
1.短期调整关系
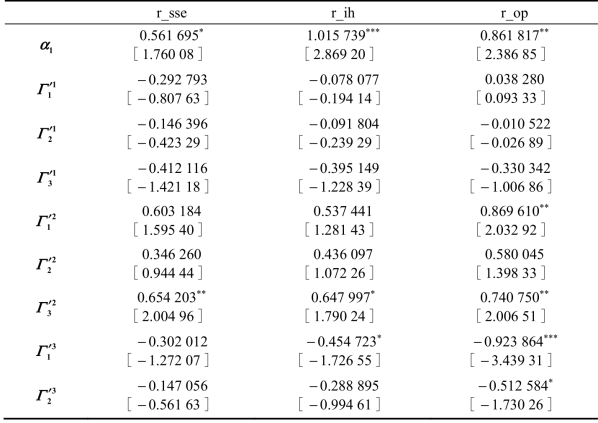
系数矩阵α为短期调整系数矩阵,代表了变量价格发生偏离时将其调整回均衡状态的速度。指数、期货和期权的短期调整系数均显著不为零,说明指数、期货和期权的短期变化都会调整三者的长期均衡关系,使其更加偏向均衡状态。
矩阵Γ为差分项系数矩阵,衡量了各变量波动对被解释变量短期变化的影响。由上表可知,疫情期间,上证50指数收益率仅受到期货滞后3期的影响,上证50股指期货仅受到自身滞后3期的影响,受到期权滞后1期的影响,上证50ETF期权受到期货滞后1期、3期的影响,受到期权本身滞后1期、2期的影响。
因此从短期影响来看,期货和期权的均值溢出效应大于指数,而期货和期权之间溢出效应的大小无法通过VECM短期调整系数得出明确结论。
表7.23 误差修正模型系数检验
续表(https://www.xing528.com)

2.协整关系
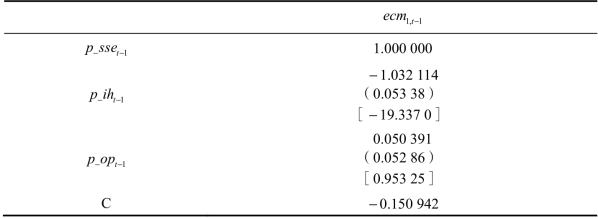
由表7.24所示,VECM模型的误差修正项为:
![]()
三个市场之间存在协整关系。
表7.24 协整方程检验
3.平稳性检验
为了保证模型运行结果的有效性,需要对模型进行单位根检验,保证模型的稳定性。根据图7.7所示,经过单位圆检验,除了VECM模型本身所假设的单位圆之外,不存在大于1的根,因此这个模型是稳定的。

图7.7 VECM模型单位根检验
VECM模型描绘了期货、期权、现货之间长期和短期之间的关系,但是系数仅仅描绘了局部静态特征,因此需要利用脉冲响应函数进行动态分析,探究某一方程随机误差项的一个标准差新信息冲击时其他市场受到的影响程度和持续时间,从而分析期货、现货、期权市场价格间的动态相关关系。图7.8反映了期货、期权和指数的脉冲响应函数图。
从总体上来看,三个市场均会受到其他市场的影响,某一市场信息的变动都会带来其余两个市场的变化,三个市场之间是相互影响的关系,但是不同市场的冲击带来的反应是不同的,具体来看:
指数对不同市场冲击的反应:根据第一个图,对于不同市场的冲击,现货市场价格在第一期做出反应,第二期反应减弱,之后反应加大,在第四期达到最大值,然后逐渐减小趋于稳定。在整个过程中,指数受到自身的影响最大,最大值约为1.523%,其次为期货,期权对指数的影响最小。
期货对不同市场冲击的反应:根据第二个图,对于不同市场的冲击,期货市场的反应便达到最大值,期货市场在第一期受到自身市场影响最大,为1.59%,其次是指数的影响,为1.56%,受到期权的影响较小,为1.55%;第二期受到冲击减小;3~5期受到的冲击逐渐增大,然后不断减少,直至趋于平稳。除第一期期货的影响最大之外,在其他时间期权均受到指数的影响最大,其次为期货,最后为期权。
期权对不同市场冲击的反应:根据第三个图,期权第一期受到自身影响最大,为1.63%,其次为期货的影响,为1.58%,受到指数影响最小,为1.56%;第二期受到三个市场的冲击均减小,3~4期冲击增大,然后受到的影响逐渐减小,直至趋于平稳。在整个过程中,除第一期期权受到自身市场的影响最大外,其他时期受到指数的冲击最大。
因此,面对市场的冲击,期货市场和期权首先反应到最大值,说明期货市场和期权相比于指数市场来说对冲击的感应时间最短,对信息的吸收速度更快;从反应程度来看,期权对不同市场的反应程度最大,其次为期货,指数的反应程度最小,说明期权吸收新信息的能力最强,指数最弱。
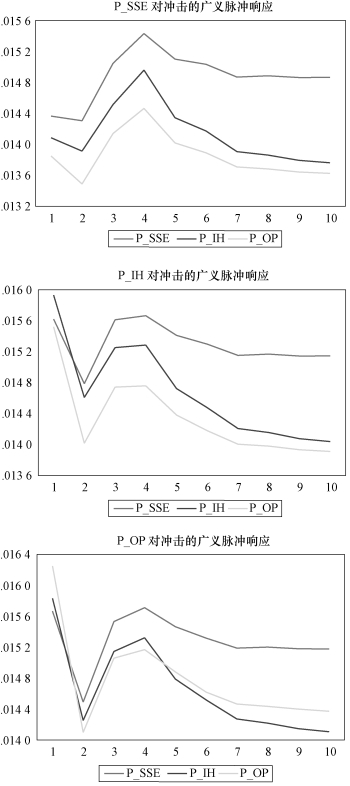
图7.8 脉冲响应函数图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




