全球金融市场变化：新冠疫情下主成分分析

本章首先使用主成分分析（Principal Component Analysis，PCA）对全球市场之间的关联性变化进行度量。主成分分析是一种将多个可能存在相关性的变量，通过正交变换转换成一组线性不相关的综合变量，以此通过几个较少的综合变量来反映原变量的信息（Muirhead，1982）。基于这一特点，主成分分析也被用作市场关联性分析的研究（Billio et al.，2012）。具体来看，定义Ri为市场 i 的股票指数收益率，i=1，2，3，…，N。RS 为样本市场总体收益率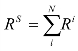，市场 i 股票指数收益率的期望E[Ri ]=μi，方差。因此样本总体方差为：

其中：

随后我们定义均值为零，互不相关的随机变量ζk，k=1，2，3，…，N，对ζk有：

其中λk为第k个特征值，进一步我们用ζk对zi进行表示：

Lik为特征值ζk作用到标准化的收益率zi的因子载荷。因此我们得到：(www.xing528.com)

至此，我们通过对方差协方差矩阵的分解将N个市场收益率转化成正交的特征向量矩阵L与对角的特征值Λ的乘积。

我们分别计算第1个、第2−10个、第11−20个、第21−30个和第31−48个主成分（PC1，PC2−10，PC11−20，PC21−30，PC31−48）对样本市场收益率解释的比率大小，并将其定义为累计风险比率（Cumulative Risk Fraction，CRF）：

更大的CRFn（n＜N）说明全球市场收益率变动更趋于同向变动，这代表全球市场之间的关联性更强。因此我们采取滚动窗口的方式分别计算PC1，PC2−10，PC11−20，PC21−30，PC31−48的CRFn并观察其随时间的变化情况。