美国中小学数学评价：五个维度的数学内容

对于中小学生，到底应该掌握哪些数学知识，获得哪些技能，世界各国教育界目前还没有一个统一的标准。美国在中小学数学评价标准中，把中小学生需要掌握的数学知识和技能划分为五个维度或模块，并对这五个维度或模块做了详细的描述。美国中小学数学内容包括五个维度：一是数的性质和运算；二是测量；三是几何；四是数据分析、统计与概率；五是代数。

（一）数的性质和运算

数的性质和运算主要考察中小学生对于数的概念的理解和运算，主要包括数的意义、数的估计、数的操作、比率和比例的推理、数和操作的性质、数的推理六个方面。

数的意义主要涉及数包含的意义，以及不同学科中数字的意义。学习数学最基本的要求就是学生能够理解数的意义，理解生活中的物体如何以数来表征。这些说起来较为简单，但真正理解则较为困难，很多学生尽管数学成绩不错，但对于数的意义则还没有真正理解，知识处于似懂非懂的层次。同时，在不同学科中，数字表示的意义也是存在差异的，这些也要求学生能够进行区分。

数的估计主要涉及不同情境下对数字进行估计，如估计房间面积等。生活中很多时候无法获得真正准确的数字，学生需要学会如何进行估计。学生对数的估计可能不是很准确，但对于问题的解决可能很有帮助。学生学会了如何估计数字，并尽可能地使自己的估计结果与实际测量结果相接近，将会减少很多不必要的投入，节省大量的时间和精力。

数的操作主要指能进行加减乘除等数的操作与运算。数是对生活的一种抽象，是生活中物体的实际表征。学生学习数学，必然要进行数的操作和运算。因此，中小学数学教育的一个重要功能就是让学生学会加减乘除这些基本的操作和运算。数的操作既是抽象的，更是具体的，学生需要从具体的操作开始，最终进入数的抽象操作。

比率和比例的推理主要指能进行比率、比例方面的推理与运算。生活中数学的运算远远比教科书中的复杂，学生不仅要学会常规数的操作和运算，还要会进行比率和比例这些非常规数的操作和运算。

数和操作的性质主要指理解奇偶数、分数、整数、虚数等，并进行相关运算。在数和操作的性质中，学生要能理解奇数和偶数的性质，能够把奇偶数结合进行操作；能够确认分数和整数，并进行分数、整数的操作；能够确认虚数和实数，并进行相关的操作。

数的推理主要指能解释数学概念，建立不同数的关系等。数的推理要求学生能够理解数的运算结果是怎么得来的，数与数之间的关系如何，数的概念包含哪些意义，如解释15为什么是奇数，17为什么是素数。7-3为什么不等同于3-7等。同时，学生要能利用数的推导和数的关系分析或解释问题，提供论据等。

（二）测量

测量主要考察使用测量工具，能够理解面积和体积等基本概念并作出求解，包括测量物理属性，测量系统（如长度、时间、温度等），测量三角三个方面。

测量物理属性主要指能比较不同物体的长度、面积、体积，并能解决物理属性测量的相关问题。学生要求能够对指定的目标进行测量，并能对不同目标之间的物理属性进行比较，得出差异。学生要能通过对目标的物理属性进行测量、比较，学会如何估计这些物理属性，并利用它们解决相关的实际问题，如地理测量、人口密度、飞行速度、频率等。

测量系统主要指能解决相同或不同测量系统的问题，如英寸与公尺的转换等。在系统的测量中，主要涉及不同测量系统之间的变化和转换，如时间中的时、分、秒等。学生既要会同一系统内的运算和转换，还要会不同系统之间的运算和转换。同时，学生还要学会如何理解任何测量都只是真值的估计值，只是对真值的一个接近，不等于真值本身。学生要学会如何确定恰当的测量精度，并知道如何获得这个测量值。学生知道如何作图来表征问题，并解决问题。(www.xing528.com)

测量三角主要指进行三角函数方面的测量与计算（4年级不做要求）。学生要能通过测量解决相关问题，如通过比较建筑物的投影来获得它的高度。学生能使用三角公式、勾股定理、余弦定理、正弦定理等解决相关的三角问题。

（三）几何

几何主要考察学生的空间推理和应用几何属性的能力，包括维度、形状，维度和形状的转换，几何图形的关系，解析几何，几何推理五个方面。维度、形状主要考察物体的几何属性，对物体给出准确的数学描述等。维度和形状的转换主要考察两维或三维物体形状的描述与分割，找出物体的相似与差异。几何图形的关系主要考察几何定理解决问题，如利用毕达哥拉斯定理解决相关问题。解析几何主要考察对几何方位、方向等的理解，如描述多个图形的切割线。几何推理主要考察对利用几何知识进行推理，如对多面体的几何属性进行推理。

（四）数据分析、统计与概率

数据分析、统计与概率主要考察描绘统计图，作出统计分析的能力，包括数据表示，数据特征，实验和抽样，概率，数据推理五个方面。数据表示主要考察对数利用各种方式进行表达和解释，如完成图表等。数据特征主要考察数据的计算、应用，解释平均数、中位数、众数等。实验和抽样主要考察如何进行抽样和进行实验分析，如分析数据偏差的原因，但对4年级不做要求。概率主要考察概率的运算，如能知道事件的独立性，计算发生的概率。数据推理只对12年级有考察要求，主要考察利用数据对事件进行推理与预测。

（五）代数

代数主要考察数的关系和函数等，包括模型、关系和函数，代数表示，变量、符号和操作，方程和不等式，代数推理五个方面。模型、关系和函数主要考察学生对代数基本知识的理解，如能描述数据模型，进行函数表达，确认、分析各种函数的关系。代数表示主要考察使用各种符号进行代数表达，如使用符号、图形、表格对不同线性表达式进行解释。变量、符号和操作主要考察对变量、表达式的操作与理解，如写出代数表达式、等式或不等式等。方程和不等式主要考察对方程和不等式的理解与运算，如对多个方程未知数的求解。代数推理主要指能利用代数来解决问题，如利用代数确认结论等。

有关数学内容各个方面的分布情况，可参看表6-1。

表6-1　数学内容分布

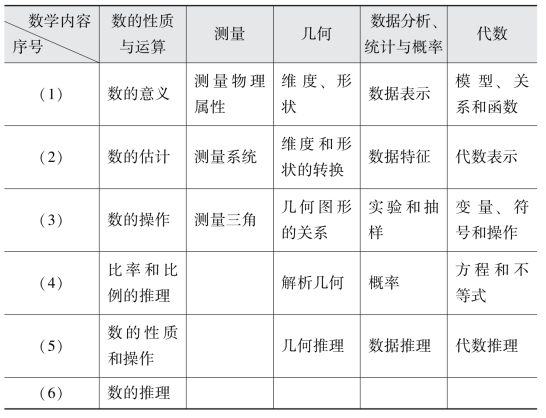
对于不同的年级，这五个方面考察比例有所区别，见表6-2。对于4年级，五个维度分布比例依次为：40%、20%、15%、10%、15%；对于8年级，五个维度分布比例依次为：20%、15%、20%、15%、30%；而对于12年级，把五个维度中的测量和几何合并为一个维度，从而只有四个维度，分布比例依次为：10%、30%、25%、35%。

表6-2　4、8、12年级数学维度评价分配比例