【摘要】：假设MCMC2的抽样次数为m＋N，则模型参数的马尔科夫链序列向量记为由于前m 次抽样用着检验序列的收敛性，因此以后N 次抽样得到的马尔科夫链序列的均值和方差作为模型参数的点估计结果，也即对统计量T i 的渐近性讨论类似于文献。(五)组合风险一步预测本节考虑组合风险VaR与CVaR的MCMC2预测问题。VaR 等同于给定时限内收益率服从的分布函数的分位数。
假设MCMC2的抽样次数为m＋N，则模型参数的马尔科夫链序列向量记为
由于前m 次抽样用着检验序列的收敛性(本文利用Geweke 统计量(Geweke，1993)判断序列的收敛性)，因此以后N 次抽样得到的马尔科夫链序列的均值和方差作为模型参数的点估计结果，也即
对统计量T i 的渐近性讨论类似于文献(Tierney，1994；Carlin and Louis，2000)。
(五)组合风险一步预测(www.xing528.com)
本节考虑组合风险VaR(Jorion，2000)与CVaR(Artzner，1997)的MCMC2预测问题。VaR 等同于给定时限内收益率服从的分布函数的分位数。若P 个收益率为r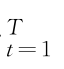
＝[r 1，t，…，r p，t
，组合收益率为∑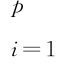
ωir i，t 其中
其中α＝0.90，0.95或0.99；CVaR 等同于组合收益率超过置信水平α的VaR 的平均损失值，也即
通过以上四步就可以预测一步风险，类似可得多步的预测算法，这是另一个值得深入的问题。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
