金融风险价值量化分析：时变Copula-GARCH-M-t

收益率时序记为r t＝(r 1t，…，r pt)；I t－1＝{r t－1，h t－1，r t－2，h t－2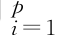，…}＝∪I i，t－1表示t时刻之前的全部信息集，其中I i，t－1＝{r i，t－1，h i，t－1，r i，t－2，h i，t－2，…}表示单个资产的信息集，h i，t＝σ2i，t为r it关于I i，t－1的条件波动率。由式(10.1)可知P个收益率的联合分布为

其中C(·|I t－1)表示条件Copula函数，F i(r i，t|I i，t－1)表示第i个分量的条件分布。

为了刻画投资者对资产时变风险的偏好程度以及收益率分布的尖峰、厚尾等特征(Engle，1987；Bollerslev，1987；Elyasiani and Mansur，1998)，我们假设r i，t满足GARCH-M-t模型，通过滤掉时变风险特征之后简化式(10.7)，以此量化收益率之间的时变相依结构特征，进而将Jondeau and Rockinger(2006)的静态Copula-GARCH 模型拓展到时变Copula-GARCH-M-t模型。

其结构设定为

其中ωi，αi，βi＞0，αi＋βi＜1，z i，t服从自由度为v i、均值为0和方差为v i/(v i－2)的T 分布，其分布密度函数为

Fi(zi，t|Ii，t－1)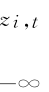＝∫fvi(s)ds，i＝1，…，p。C(·|It－1)表示自由度为η 的具有时变相关系数的条件t-Copula函数。这里仍沿用无条件Copula函数的方式书写。由式(10.2)得Copula密度函数(www.xing528.com)

其中f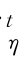Rt 表示自由度为η 和时变相关系数矩阵为Rt＝(ρi，j，t)p×p的多元t分布。依据TseandTsui(2002)，Rt 的演化方程设定为

由式(10.10)得到式(10.8)中资产收益率的联合密度函数

及似然函数

对多元模型(10.8)而言，当Copula函数和边缘函数具有复杂的解析式时，式(10.12)和式(10.13)也会变得复杂，这样在通过最优化高维参数变量的似然函数的过程中，可能使得MLE 方法和IFM 方法变得效率低下(Liu and Luger，2009)。为此本文从贝叶斯分析的角度认为，在实现假设模型参数的分布情况下，通过样本数据模拟模型参数的马尔科夫链，不断地对参数的先验分布进行校正，最终寻找到原来参数的真实分布及其贝叶斯点估计，这样降低了高维参数问题的优化难度。依据已有文献利用贝叶斯方法估计GARCH等随机模型参数时的方法(Bauwens and Lubrano，1998；Nakatsuma，2000；Tsay，2005；Ardia，2009)，可以将均值方程和波动率方程中的参数分开构建收敛的马尔科夫链，也可以将模型的所有参数构成一个多元参数向量，基于多元联合分布抽样的方式同时构建多维马尔科夫链。因此本文基于IFM 法的分步思想，将边缘模型GARCH-M 的参数和时变Copula参数分开构建马尔科夫链，提出模型(10.8)中全部参数估计的两步MCMC抽样方法。