金融风险价值量化分析: Copula尾部指数变化

记随机变量x i(i＝1，…，p)的边缘分布、边缘密度分别为u i＝F i(x i)和f i(x i)＝du i/dx i。根据SKlar定理(Sklar，1959)，X＝[x 1，x 2，…，x p]的联合分布F(x 1，…，x p)、边缘分布与F的Copula函数C(u 1，…，u p)的关系为

由于u i 服从[0，1]上的均匀分布，因此C 也表示单位超立方体[0，1]p 中的一个多元分布函数。比如，高斯Copula函数中R ＝(ρi，j)p×p 表示相关系数矩阵，t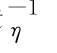表示自由度为η 的t分布的逆函数。当η→∞时，t-Copula退化为高斯Copula。对式(10.1)两边求导，得到多元Copula密度为

据Nelsen(2006)可知Copula函数唯一地决定了相依结构的局部特征。在金融分析中学术界多用上(下)尾部指数来量化金融市场或者资产价格的同涨(跌)现象。对于二维Copula函数而言，上尾λu 和下尾指数λl 分别定义为

将式(10.2)代入式(10.3)进一步可得(www.xing528.com)

经计算可知，高斯Copula的两个尾部指数λu＝λl＝0，t-Copula的尾部指数为

其中tη＋1表示自由度为η＋1的学生t分布，ρ 表示静态相关系数。对于动态(时变)相关系数ρt 而言，时变尾部指数的计算公式为

资产的时变相关性决定了相依结构的尾部特征的变化趋势(Cherubini等，2004)。由于t-Copula函数能很好地量化尾部相依结构，因此式(10.6)计算的时变尾部指数能很好地量化资产同涨跌的变化趋势。进而在运用GARCH 类模型滤掉收益率波动特征后对新息序列构建相依结构模型，这样时变尾部指数才能较好地量化资产价格的极端行为。为此下面构建时变Copula-GARCH-M-t模型。