金融风险价值量化分析：时变Copula-GARCH-t模型

记P个资产收益率时序为r t＝(r 1t，…，r pt)，若t时刻之前的先验信息集为I t－1＝{r t－1，h t－1，r t－2，h t－2，…}＝∪pi＝1 I i，t－1，其中I i，t－1＝{r i，t－1，h i，t－1，r i，t－2，h i，t－2，…}，h i，t为r it关于单个资产先验信息集I i，t－1的条件波动率。C(·|I t－1)表示p维条件Copula函数，F i(r i，t|I i，t－1)为第i个分量的条件分布。由Skalar(1959)定理，可知P个资产收益率的条件联合分布为

众多实证研究表明资产收益率序列服从GARCH(1，1)模型。Bollerslev(1987)指出用学生t分布比正态分布更能体现金融时间序列的尖峰、厚尾等特征。这里也假设r i，t满足该模型，由此滤掉单个序列的时变波动特征后，我们提出时变Copula-GARCH(1，1)-t模型(简记为Copula-GARCH-t)，用以描述P个资产的时变相依结构，因此模型设定为

其中ωi，αi，βi＞0和αi＋βi＜1确保条件波动率序列的平稳性。考虑新息z i，t服从自由度为v i、均值为0和方差为v i/(v i－2)的学生t分布，也即z i，t的分布密度为

式(9.8)对应的条件边缘分布为F i(z i，t|I i，t－1)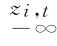＝∫f vi(s)ds，i＝1，…，p。Copula函数C(·|I t－1)的密度c(·)设成自由度为η 的时变t-Copula，式(9.4)的Copula密度为

其中f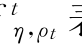表示自由度为η 和时变相关系数矩阵为ρt＝(ρi，j，t)p×p 的多元学生t分布，ρi，i，t＝1，f vi 由式(9.9)给出。类似于Tse和Tsui(2002)等的多元Copula-GARCH 模型中时变相关系数矩阵方程，假设ρt 的演化方程为

其中a≥0，b≥0，ρ 是主对角元都为1而其他元为静态相关系数构成的正定阵，Ψt－1是p×p 矩阵，t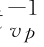(f v p(z p，t)))，0≤a，b ≤1，a＋b ≤1和－1≤ρi，j，t ≤1，因而不必运用Patton(2006)及Dias and Embrechts(2004)等人对时变相关矩阵的演化方程进行的Logistic变换，以此确保ρi，j∈(－1，1)。(https://www.xing528.com)

由式(9.10)得到条件联合密度

及似然函数

其中θ＝{[μi，ωi，αi，βi，v i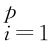，[a，b，ρ，η]}，x t＝(x 1，t，…，x p，t)，ρt 由式(9.11)给出。

由式(9.12)和(9.13)得到模型参数的IFM 估计。这里存在的问题是IFM 方法并没考虑到参数的先验分布受样本信息的后验影响，因此我们顺便推导参数的条件后验分布密度函数，然后从贝叶斯学习的角度，分析模型参数的贝叶斯统计推断过程。同时将这两个估计结果进行比较，以此说明后者是一种较为实用的新方法以及体现出MCMC方法对该模型在参数估值上的优势。