Copula函数小波收缩估计结果

本节将一维分布的小波收缩估计量引入Copula函数的统计推断。利用一维小波函数和尺度函数，采用张量积算子构建高维小波函数(Cohen 等，1993)。对尺度j 0 ∈N，函数空间L 2(R)的一组基为{φj 0，k} ∪{ψj，k}，其中φj 0，k(x)＝2j 0φ(2j 0 x－k)、ψj 0，k(x)＝2j 0ψ(2j 0 x－k)。对d维向量X＝[x 1，x 2，…，x d]，定义多元尺度函数φj，k(X)和小波函数ψij，k(X)分别为

其中i＝[i 1，…，i d]，i n＝0或1(n≠0)，记S＝{0，1}d\{(0，…，0)}，i∈S。易见，j 级尺度空间L 2(R d)的一组基可由1个尺度函数和(2d－1)个小波函数构成。于是，L 2(R d)的一组基函数表示为

其中I j 0＝{1，…，2j 0}d，I j＝{1，…，2j}d。因为集合E j 0 中的函数均具有正交性，所以任意的Copula函数h(X)∈L 2(R d)在该集合上可以展开为

其中αj 0，k ＝∫Rd h(X)φj 0，k(X)d X，β ＝∫Rd h(X)ψ(X)d X 。我们利用式(4)及密度函数的性质，得到小波系数的矩法估计为

其中j，t＝(x j，t)，(i＝1，…，d；t＝1，…，T)，边缘分布的小波收缩估计量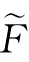(x j，t)由式(8.8)给出。(www.xing528.com)

式(8.9)表明多元联合分布的总体特征可以分解成尺度j 0∈N 上的趋势特征和若干个细节特征。类似一维分布的软阈值小波收缩估计方法，总可以在某个尺度上截断式(8.9)中可以忽略的细节成分。关于这种截断估计量的误差收敛性问题的分析结论可见Donoho等(1993)、Kerkyacharian和Picard(2001)及Chesneau(2008)。为了展示相依结构在不同尺度上的局部特征，Genest等(2009)采用这种思想研究了Copula函数曲面的线性截断估计问题，而Autin 等(2010)更进一步将其拓展到了Maxset(最大集)优化的BESOV 空间，解决了Copula函数的非线性截断估计问题。其中存在的问题是并没有考虑到数据质量问题，运用了一维经验分布代替真实的边缘分布，忽略了数据中的噪声成分，这使得估计结果不准确。为了弥补这个缺陷，我们考虑用一维分布的小波收缩估计量代替经验分布，构建Copula函数的小波收缩估计量为

其中j 0，k＝j 0，k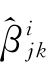＝(||－λ)sgn)，sgn为符号函数，阈值λ＝，0≤j 0＜J max，最大尺度J max＝0.5 log2(T/log T)。式(8.11)的估值误差定义为均方积分误差(MISE)：

注1：光滑度为s 的d 维Copula 密度的MISE(，c)等同于r T ＝(log(T)/T)2d/(2s＋d)，该结果的证明类似于Autin等(2010)，关于λ 和j 0 的选取方法见Genest等(2009)。

注2：当＝I(||≥λ)，式(11)变成Autin等(2010)的非线性阈值估计量；当＝0，式(11)等同于Genest等(2009)的线性截断估计量。这两种方法对边缘分布的估计都用到了样本的经验分布，而本章采用边缘分布的软阈值小波收缩估计量(x)代替经验分布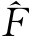(x)。这样避免了噪声对真实Copula函数参数估计的影响，进而为Copula函数选择的小波方法提供了理论支撑。