小波收缩估计量用于金融风险价值量化分析

金融相依结构建模中，由于金融数据往往受到市场微观结构噪声污染，拟合边缘分布模型的误差较大。为此本章结合小波函数的局部自适应能力和变焦功能，引入一维分布函数的小波收缩方法(Donoho，1993)估计边缘分布相关的非参数模型。假设X i(i＝1，2，…，d；d≥2)的边缘分布F i(x i)满足

式(8.5)中u i＝(T＋1)－1∑Tj＝1 I(X i，j≤x i)，w i 为维纳过程，σ≥0显示噪声对真实分布的影响程度。

假设尺度函数φ 和小波函数ψ 有较好的正则性，由父小波φ 和母小波ψ生成的正交基分别记为φj，k＝2j/2φ(2jx－k)和ψj，k＝2j/2ψ(2jx－k)，则存在正整数τ 使得函数系ζ＝{φj，k(x)，k＝0，…，2τ－1；ψj，k(x)，j＝τ，…，∞，k＝0，…，2j－1}构成空间L 2(R)的一组正交基。因此，对任何l≥τ，平方可积的一维分布函数F(x)∈L 2(R)在小波基函数构成的集合ζ 中展开为

代入式(8.6)，可得：(www.xing528.com)

对于样本观测值X i，t(i＝1，…，d；t＝1，…，T)，u i，t ∈(0，1)，令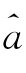l，k 和j，k 分别为－∫w iφl，k(x)dx和－∫w iψj，k(x)dx 的估计值，即噪声的小波估计量，则小波系数的矩法估计为：

由式(8.7)计算出的小波系数受到噪声污染，为了得到边缘分布F i(x i)的最佳估计量，这里应用Donoho等(1993)提出的几种阈值规则，对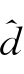jk进行阈值收缩，得到一维分布的小波收缩估计量

式(8.8)中0≤j 0≤l，l≤j max＝2 log(T)，阈值参数λ＝log(T)/T，按收缩的方式，将阈值记为硬阈值和软阈值N∈{H，S}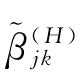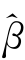＝jk I(|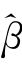jk|≥λ)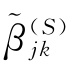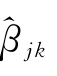，＝(||－λ)sgn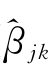)。因此基于这两种阈值规则，式(8.8)给出边缘分布的两种小波收缩估计量。如果密度函数具有紧支撑性，那么该估计量具有渐进无偏性(Kerkyacharian和Picard，2001；Chesneau，2008)。由于软阈值规则具有较强的局部自适应能力，拟合边缘分布时，均方误差的收敛性较快，大样本下的渐近性较好(彭选华和傅强，2011)，因此软阈值小波收缩估计量更适合消除边缘分布特征对Copula函数选择的影响。