金融风险价值量化分析及应用

仿真算例表明基于非线性阈值的多元Copula密度估计有三个优点：(1)减少了参数族Copula建模的盲目性；(2)在样本容量大的情况下，减少了极大似然估计的计算量和全局优化的搜索难度；(3)高斯Copula密度的还原是对真实Copula相依结构的高精度刻画。

有鉴于此，下面我们将本方法应用于量化资产组合风险VaR 及CVaR(Jorion，1997)。组合风险VaRΔt(α)定义为组合收益率r p，t在投资期[T，T＋Δt]内的θ分位数，其中表示组合内单个资产的时变收益率，ωi 为资产权重。也即投资组合的条件VaR 为CVaRΔt(θ)＝－E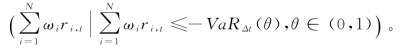

依据已有文献的研究结论可知CVaR更能较准确地量化金融风险(Rockafellar等，2002)，在此考虑资产投资组合CVaR 的计算结果，仅仅比较基于正态Copula密度与其还原的Copula密度的CVaR变化特征，以此说明本文方法应用于对资产之间相依结构特征识别是资产组合风险管理中重要的一环。

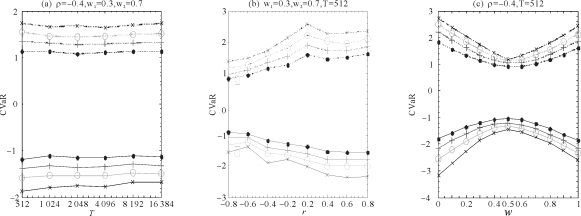
图7.2给出了CVaR 的仿真结果，(a)～(c)分别展示了基于正态Copula的资产组合分别在置信水平(1%，2.5%，5%，10%)多头和(99%，97.5%，95%，90%)空头的CVaR，其中(a)为Copula参数为－0.4、资产权重为0.3和0.7时CVaR 随样本容量的变化关系；(b)为样本容量为512、资产权重为0.3和0.7时CVaR 随Copula参数的变化关系；(c)对应了Copula参数为－0.4、样本容量为512时CVaR 随资产权重的变化关系。(e)～(f)分别展示了基于小波还原的正态Copula的产组合分别在置信水平(1%，2.5%，5%，10%)多头和(99%，97.5%，95%，90%)空头的CVaR，其中(d)为Copula参数为－0.4、资产权重为0.3和0.7时CVaR 随样本容量的变化关系，(e)为样本容量为512、资产权重为0.3和0.7时CVaR 随Copula参数的变化关系，(f)对应了Copula参数为－0.4、样本容量为512时CVaR 随资产权重的变化关系。(www.xing528.com)

图7.2　资产组合CVaR 的量化分析

通过分析图7.4后发现：(1)(a)与(d)表明随着样本容量变化，CVaR 的估值趋势具有稳健性；(2)(b)与(e)表明在样本量和投资权重确定的情况下，资产组合CVaR 估值与Copula参数变化不具有对称性；(3)(c)与(f)表明在样本量和Copula参数确定的情况下，资产组合权重的变化使得组合风险CVaR 的变化具有对称性。当最优资产组合权重为0.5时，空头风险CVaR达到最小值，多头风险CVaR 达到最大值。结果非常符合事实，即在单个资产收益服从高斯分布且资产之间存在正态相依结构时，最佳投资组合就是平均配置资产。

总体而言，尽管CVaR 的估值存在个别差异，但Copula密度的小波还原是对资产之间真实相依结构的高精度刻画，这进一步验证了理论结果及其应用的可行性。