金融风险价值量化分析：算法设计与实现

估计精度分析的计算原理为：从边缘变量的经验分布开始，运用小波函数逐级分解经验Copula，利用局部阈值规则对经验小波系数逐级修剪，进一步实施小波逆变换得到局部光滑的曲面，不断地调整小波分解尺度，直至获得最佳的空间曲面为止，最后将该曲面规范化结果作为潜在Copula密度的小波局部阈值估计量。具体计算程序如下：

步骤3:利用塔式算法，计算尺度j的小波系数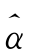j，k和尺度系数；

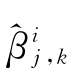步骤4:利用式(7.12)得到局部阈值小波系数δ；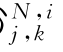

步骤5:利用塔式算法在适当尺度j＝j 0(J n ≤j 0≤J max)上重构Copula密度

步骤6:利用网格近似计算均方积分误差

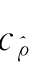其中网格结点取为{0，1，2，…，J max＋1}d ⊂[0，1]d，N 表示最佳的小波局部阈值估计量， 表示样本真实的参数Copula密度函数。(www.xing528.com)

关于步骤6说明两点：

(1)对已知样本数据适合的参数Copula模型而言，式(7.31)度量了小波局部阈值估计量的估值精度；

(2)对未知样本数据适合的参数Copula模型而言：当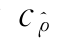 为拟合的最佳参数Copula模型时，式(7.31)度量了小波局部阈值估计量与最佳参数Copula之间的最小偏差；当 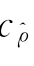不是最佳的参数Copula模型时，以式(7.31)的方式在参数Copula类中筛选出样本数据之间最匹配的参数Copula模型。

综合以上两点，本文认为：如果经典方法的估计结果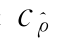不能很好地量化样本数据之间相依结构的局部特征，那么可以基于小波局部阈值估计量最小化式(7.31)，从而实现对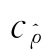的参数校正。