金融风险价值量化分析的主要结果-函数空间范数、精度分析

依据Vidakovic(1999)可知L 2([0，1]d)⊆B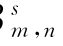([0，1]d)，由小波系数定义的Besov空间B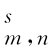的三个特征参数分别是：s 表示该空间内函数的光滑度；m，n(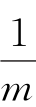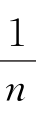＋＝1)为空间的范数指标。接下来，定义7.1给出了Copula函数空间的范数类型，定义7.2进一步界定了精度分析的函数空间，定义7.3还将Besov球内两个Copula密度函数之间的均方积分误差(MISE准则)作为刻画估值精度的指标量。

定义7.1:(Besov 范数)假设具有一定光滑度的密度函数c(u)∈B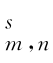([0，1]d)，若尺度系数αj 0，k ＝∫[0，1]d c(u)φj 0，k(u)du 和小波系数β 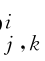＝∫[0，1]d c(u)ψ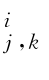(u)du，则c(u)的(m，n)-范数定义为

定义7.2:(Besov球)令Ωτ(Aτ)表示以Holder连续性指数为τ 的密度函数c(u)构成半径为Aτ 的函数集合，则Besov球定义为

定义7.3:(MISE准则)假设任意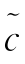(u)、c(u)∈Ωτ(Aτ)，则均方积分误差定义为

Cohen等(2001)、Kerkyacharian and Picard(2002)和Chesneau and Christophe(2008)等认为在利用minimax优化方法得到最优估计量时，MISE的收敛速度受到函数空间特征的影响。因此Autin(2006)提出的maxset优化方法比minimax方法得到的收敛速度更具有可控性，为此本章利用maxset优化方法分析MISE准则的上边界，进而得到小波局部阈值估计量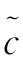(u)对真实Copula密度c(u)的估值精度。记N∈{HL，SL}，那么两个非线性局部阈值估计量的MISE记为

利用式(7.4)中数学期望的性质，得到MISE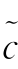N，c)＝E‖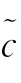N－c‖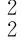。显然Besov球中MISE 的上界M 必然存在，而且M 与空间的光滑度指标和样本容量有关，因此我们给出式(7.13)的估值精度结论如下(www.xing528.com)

定理7.1表明估值精度的等价量r T(s，d)＝(log(T)/T)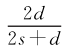取决于样本容量T 及Copula密度函数的光滑度指数s 和维数d。进一步分析得到三点结论：

①当s 和d 都是确定的常数时，只有T 影响到估值精度，而且当T 足够大时估值精度越高，小波局部阈值估计量是真实Copula的渐进无偏估计量；

②当T 和d 都是确定的常数时，只有S 影响到估值精度，而且当S 越大时估值精度越高，Copula密度曲面的解析性越好，这表明该估计量更能刻画样本潜在的局部相依结构；

③当T 和S 都是确定的常数时，只有d 影响到估值精度，当d 越大时估值精度越差，通过降低多元Copula密度的维数之后，估值精度才能达到可接受的数量级。