记Φ＝φj 0，k(X)、ψ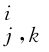
(X)，结合式(7.4)、(7.5)和(7.6)，可得多元Copula密度函数的多尺度展开为
αj 0，k＝E h(φj 0，k(F(X)))和β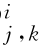
＝E h(ψ
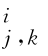(F(X)))。如果X＝[x 1，x 2，…，x d]的T 个实现值为{x
}
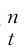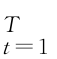(n＝1，…，d)，得到式(7.8)的样本估计为
其中系数的样本估计量为
在相依结构建模过程中，由于边际分布F 1，…，F d并非事先知道，因此不能直接计算式(7.10)的值，本章类似Genest(2009)将经验分布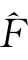
1(x
)，…，
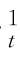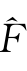d(x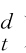
)代替边缘分布函数，得到经验系数为
式(7.9)表明可以直接利用塔式算法重构Copula密度c(u)。由于样本数据可能含有噪声成分，因此根据式(11)算出的系数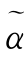
j 0，k和
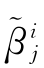，k也受噪声影响。譬如，在高频金融分析中资产价格可能受宏观经济信息的冲击，使得小波系数失真，因而有必要对经验系数
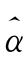j 0，k，
)进行阈值修剪。Donoho 等(1996)认为线性阈值(L)和非线性阈值(N)广泛适用于修剪小波系数。线性阈值中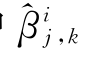
＝0保留趋势成分，但这样处理后得到的Copula密度函数并不能刻画具有复杂特征的样本数据之间潜在相依结构的局部特征。因此本文利用包含局部硬阈值(hard)和软阈值(soft)等非线性阈值规则修剪经验系数。在线性阈值规则基础上适当选取阈值参数λj，处理系数
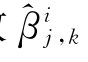为
阈值参数λj 是一个局部变量，对同一尺度上的小波系数按同一标准修剪，这样不同程度地展示了潜在Copula的局部特征，由此得到Copula密度的局部硬阈值估计量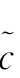
HL和局部软阈值估计量
SL分别为(www.xing528.com)
式(7.13)展示出三个优点：
1.该Copula密度近乎无损地量化了相依结构的局部特征；
2.非线性阈值规则起到了数据压缩和局部降噪的作用；
3.尺度指标的变化，体现了小波函数逐级自适应性地检测出潜在相依结构特征，因而估计量也变尺度地展示了样本数据之间潜在相依结构的局部特征。
式(7.8)、(7.9)、(7.13)之间的差异表明，c(x)
(x)
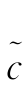HL 和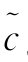
SL 都与尺度指标(j n，J n)和阈值参数λj有关
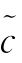HL(或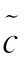
SL)与c(x)之间的估值偏差可以分解为
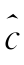(x)与c(x)之间的随机误差和
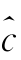(x)与
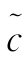HL(或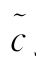
SL)之间的尺度截断误差，这两种误差的精度直接反映了小该估计量对样本潜在相依结构特征的量化效果。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
