【摘要】：在边缘分布独立的条件下，利用式(7.1)及多元密度h＝d H/X，可得任意 Φ ∈ L 2 关于c 的期望为 E c(Φ) ＝∫[0，1]dΦcdu，由式(7.3)得式(7.4)给出了Copula密度的一个重要的变换关系，Copula分为参数Copula簇和非参数Copula簇。Cherubini等给出Copula的估计方法主要有精确极大似然估计、完全极大似然估计、两步极大似然估计、半参数极大似然估计及非参数核函数估计等。
假设{x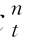
}
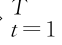(n＝1，…，d)表示d维随机变量X＝[x 1，x 2，…，x d]的样本实现值，其中x n 具有单调递增的分布函数u n ＝F n(x n)，边缘密度函数f n(x n)＝d F n(x n)/dx n.若X 的密度h(X)∈L 2([0，1]d)，由Skalar(1959)定理，知存在多元Copula函数C(·)使得
对任意的H(X)，式(1)均能提取边缘分布F n 和Copula函数C(u)(u＝[u 1，…，u d]).如果已知F n 和C(u)的解析式，可根据式(7.1)得到H(X).其中不必假设边缘分布都具有相同的函数形式以及C(u)的选取不受制于边缘分布，因此这使得Copula函数成为相依结构建模与风险分析的实用方法。
在边缘分布独立的条件下，利用式(7.1)及多元密度h(X)＝∂d H(X)/∂X，可得(www.xing528.com)
任意 Φ(u) ∈ L 2([0，1]d) 关于c(u) 的期望为 E c(Φ) ＝∫[0，1]dΦ(u)c(u)du，由式(7.3)得
式(7.4)给出了Copula密度的一个重要的变换关系，Copula分为参数Copula簇和非参数Copula簇。Cherubini等(2004)给出Copula的估计方法主要有精确极大似然估计、完全极大似然估计、两步极大似然估计、半参数极大似然估计及非参数核函数估计等。与这些已有方法不同的是，本文对具有复杂特征的样本数据潜在相依结构的估计问题，提出一种新方法用以自适应地量化相依结构的局部特征。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
