金融风险价值分析：美股、亚洲股市和新兴市场指数的实证应用

本节选取美国标普500指数(SP500)、日经225指数(N225)和上证指数(SSEC)为实证对象，其中SP500代表世界成熟股市指数，N225代表亚太地区成熟股市指数，SSEC代表新兴市场指数，时间跨度为1999年10月26日至2010年1月12日。为了保证交易日期的同步性，使得相依结构的小波估计量具有局部可比性，故实际平行观测样本为2132个，选用DB8小波识别三个不同性质市场指数之间潜在的局部相依结构，同时筛选出最佳的参数Copula模型。利用Wav Lab8.5工具箱编写程序：执行算法步骤1～5，实现对样本相依结构的小波线性估计，结果见图6.1～6.2和表6.1；执行算法步骤6～7，实现最优化筛选参数Copula模型，结果见表6.2和图6.3。

图6.1是对(6.14)式的直观解释，其中(a)分解尺度j＝1，2，3，4及网格为323个；(b)图6.1(1)A 4表示经验Copula在分解尺度4上的趋势；图6.1(6)ECD 表示三指数收益率之间的经验Copula；图6.1(2)D4表示经验Copula在分解尺度4上的局部细节；图6.1(3)D3表示经验Copula在分解尺度3上的局部细节；图6.1(4)D2表示经验Copula在分解尺度2上的局部细节；图6.1(5)D1表示经验Copula在分解尺度1上的局部细节。

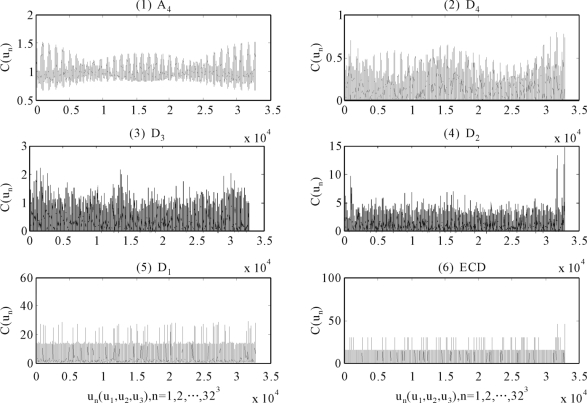
图6.1　三指数收益率相依结构的多尺度分析

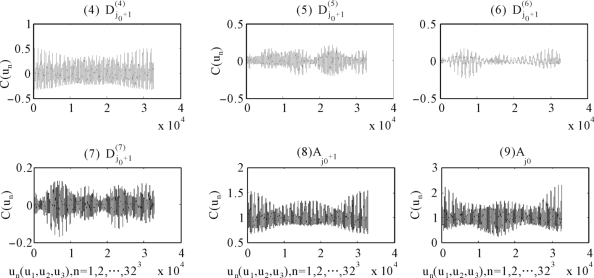
图6.2　三指数收益率相依结构的多尺度级联分解

图6.2是对(6.6)式的直观解释，其中(a)分解尺度j＝0，1及网格为323个；(b)图6.2(1)－(7)表示经验Copula ECD 在分解尺度j 0＋1上分解成的7个细节成分；图6.2(8)为经验Copula在分解尺度1上的趋势；图6.2(9)为经验Copula在分解原尺度j 0上的趋势。

表6.1给出了不同分解尺度上小波线性估计量的均方积分误差。这些数据表明随着尺度j 0增加，小波线性估计量对标普500指数、日经225指数、上证综合指数等三者之间经验Copula的估值均方积分误差越来越小，因而潜在相依结构的最佳估计量取为尺度j 0＝1的小波线性估计量，详见图6.3(8)。

表6.1　基于小波收缩估计量的均方积分误差

(www.xing528.com)

表6.2给出了基于最佳小波估计量的参数Copula筛选结果及其均方积分误差(由式(6.15)给出)，其中c1～c6依次对应于正态N-Copula族、学生TCopula族、冈贝G-Copula族、凯莱C-Copula族、富兰克F-Copula族和这五个族构成的混合Copula族，详见图6.3(1)至(6)。

表6.2　基于小波线性估计量的Copula参数最优化与最小均方积分误差

注：Ci－表示常见参数Copula，i∈{N、T、G、C、F}，wi－表示混合Copula(C6)中Ci的权重。

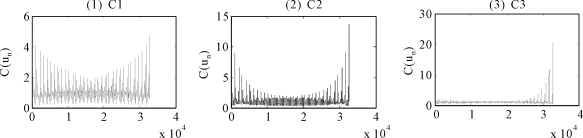
图6.3　指数收益率相依结构最优化的参数Copula模型

表6.2中MISE显示每个单一参数Copula的估值误差都比混合Copula族的大，说明混合Copula族是所有参数Copula族中最好的Copula模型，用以刻画三个股市指数之间潜在相依结构特征。混合参数Copula族中对应单一参数Copula的权重度量了其对样本相依结构描述的最大贡献力度，权重还体现了混合参数Copula族内单一参数Copula之间的和谐性，从而使得混合参数Copula族中多个单一参数Copula共同增强了相依结构的建模精度。这证实了，混合Copula族整合了所有单一参数Copula族的共同优点，单一参数Copula族的最优化估值与其在混合参数Copula族的估值有明显的差异，这种差异在于后者包容了前者的不足，从而实现对样本潜在相依结构的最佳建模。

图6.3(8)为样本潜在相依结构在最佳尺度j0＝1的小波线性估计量；图6.3(7)是样本的经验Copula；图6.3(1)～(6)分别是以最佳小波线性估计量为基准对参数Copula的最优化估值，顺序依次为高斯Copula、学生T-Copula、冈贝G-Copula、凯莱C-Copula、富兰克F-Copula及其混合参数Copula。

图6.3表明混合参数Copula是对样本潜在相依结构的最佳参数化建模。我们发现最佳的混合参数Copula清楚地展示了样本的相依结构，但视觉效果不及小波线性估计量，某些局部结构特征并不能准确地被展示出来，这是参数Copula的不足之处，然而小波线性估计量正好弥补了这个缺陷。小波线性估计量是对美国标准普尔500指数、日经225指数、中国上证综合指数等三者收益率之间相依结构的真实刻画。这为真确认识三大经济体在经济金融方面的关联性提供了一种重要的多尺度工具。