金融风险价值量化分析教程：计算步骤简介

小波给出了随机变量相依结构识别与统计推断的新方法。本文三维估计量的计算原理为：从标准化秩序统计量(R 1，i/T，R 2，i/T，R 3，i/T)的直方图开始，运用三维小波函数对参差不齐的经验直方图逐次磨光，得到局部光滑的空间曲面，不断地调整小波分解尺度，直至获得最佳空间曲面，最后对该曲面进行规范化后作为潜在Copula的小波线性估计量。计算步骤如下：

步骤1:计算分解尺度J max(N ＝2Jmsx ≤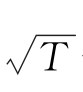＜2J max＋1)，表示长度为T 的样本序列的最大分解尺度。

步骤2:将立方体[0，1]3 等分成N 3 个网格，计算每个小正方体内(U 1，i，U 2，i，U 3，i)的频率，并视为尺度J max的经验尺度系数。也即，

步骤3:为了避免网格的边界效应，对称延拓矩阵 A ＝

步骤4:对B进行小波变换，提取其(2，2，2)位置的块作为A 的小波分解，在尺度j 0＝1，2，…，J max上，分别重构Copula密度C的线性估计量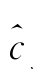j 0为

步骤5:选取最佳的c*＝j 0 作为样本潜在Copula密度C 的小波线性估计量。(www.xing528.com)

步骤6:基于网格近似计算均方积分误差：

其中，c 为真实的Copula，网格个数为N 3＝32×32×32，式(6.15)是对式(6.12)的离散化处理。

步骤7:基于最佳小波线性估计量c*最优化赛选Copula模型：

其中cθ 表示一类参数Copula模型，c*为样本真实相依结构的最佳小波线性估计量。这里的参数Copula模型(Cherubini等，2004)[4]包含：Gaussian、Student、Gumbel、Clayton、Frank以及混合Copula，分别记为：c 1 ＝{c ∈Nθ，θ ∈(－1，1)3}、c 2＝{c∈Tθ，θ∈(－1，1)3×[1，∞)}、c 3＝{c∈Cθ，θ∈[0，20]}、c 4＝{c∈Gθ，θ∈[0，20]}、c 5＝{c∈Fθ，θ∈[－20，20]}、c 6＝{c∈Mθ|Mθ 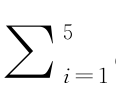＝ωic i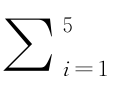ωi ＝1]}。

对小波函数的选择而言，DB8小波(S Mallat，1998)[13]具有相位保持功能，在多尺度分析中，不存在相位平移，其紧支撑性使得计算复杂度降低，后文以此为实证研究的小波函数，其他小波函数可以类似操作，其数值结果可能存在差异，但不会改变方法的实质。