【摘要】：记一维尺度函数和小波函数分别为φ 和ψ 以及其伸缩和平移变换为若x∈R 和k∈Z，则φ 的正则性和紧支撑性确保φj，k是L空间的正交函数系。任意j∈N，k＝∈Z 3，利用φ 和ψ 的张量积生成对应的三维尺度函数φj 0，k和小波函数ψ，i＝1，2，∧，7。小波对相依结构的级联分解，有助于从多时间尺度方向上深度剖析随机变量之间的相依结构的变化趋势和局部细节特征。下面给出三维Copula密度的小波估计方法。
小波技术已经成功地应用于不同的学科研究领域，比如信号检测、图像处理及统计学等。记一维尺度函数和小波函数分别为φ 和ψ 以及其伸缩和平移变换为
若x∈R 和k∈Z，则φ 的正则性和紧支撑性确保φj，k(x)是L(R)空间的正交函数系。任意j∈N，k＝(k 1，k 2，k 3)∈Z 3，利用φ 和ψ 的张量积生成对应的三维尺度函数φj 0，k和小波函数ψ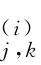
，i＝1，2，∧，7。也即：
集合{φj，k，ψ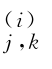
：i＝1，2，∧，7；j≥j 0；k∈Z 2；j 0∈N}是空间L 2(R 3)的一组正交基，则任意三元函数h(x 1，x 2，x 3)在尺度j 0 分解为
式(6.3)中趋势成分为A j 0 h(x 1，x 2，x 3)＝
αj 0，kφj 0，k(x 1，x 2，x 3)和细节成分为(https://www.xing528.com)
其中αj 0，k、β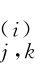
(i＝1，2，∧，7，j≥j 0，k＝(k 1，k 2，k 3)∈Z 3)分别是尺度系数和小波系数，也即
由式(6.4)易见三元函数的小波级联分解就是尺度j 0＋1的趋势等同于尺度j 0的趋势成分加上水平、垂直和对角等方向上的细节成分，也即：
式(6.6)表明小波级联分解保留了尺度之间一贯的主体趋势特征和局部异质特征。小波对相依结构的级联分解，有助于从多时间尺度方向上深度剖析随机变量之间的相依结构的变化趋势和局部细节特征。下面给出三维Copula密度的小波估计方法。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
