金融风险价值量化分析：利用Copula模型识别潜在相依结构

本文选取美国国债指数(TNX)、标普500 指数(SP500)、中国国债指数(CNGZ)和上证指数(SSEC)为实证对象，应用DB8小波线性估计量识别样本之间潜在的局部相依结构特征。时间跨度为2003年3月25日至2010年4月19日，数据下载于雅虎财经网站(http：//finance.yahoo.com)及广发证券客户端(至强版V6.02)。根据Hamao等(1990)[22]的结论，如果某一市场在某日没有交易，在同一实证模型中删去另一市场在该日的交易数据来进行计量分析，则不会影响研究结果的正确性。因此，为了保证交易日期的同步性，使得相依结构的小波估计量具有局部可比性，故实际观测值为1 611个，样本描述统计与分布特征见表5.1。

表5.1　收益率序列描述性统计量及分布特征检验

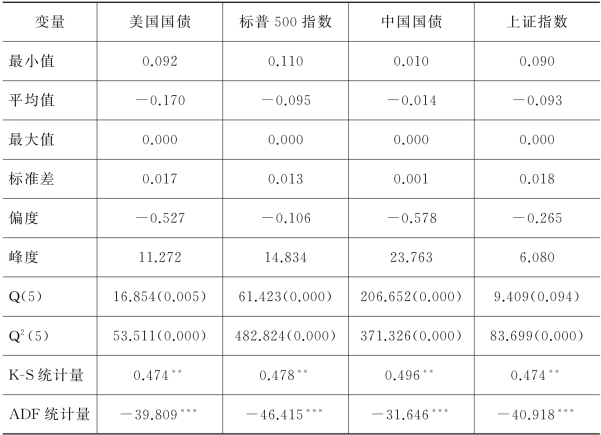
注：Q(n)和Q2(n)统计量分别检验收益率及其平方滞后1至n阶的自相关系数和是否联合为0。在序列无关的假定下，两个统计量服从χ2(n)分布，其中χ2(5)的5%临界值分别是11.070，(*)表示概率值。“**”表示Kolmogorov-Smirnov统计量5%置信水平显著，即收益率均不服从标准正态分布。“***”表示ADF 统计量5%置信水平显著，即样本序列一阶平稳，不存在单位根。

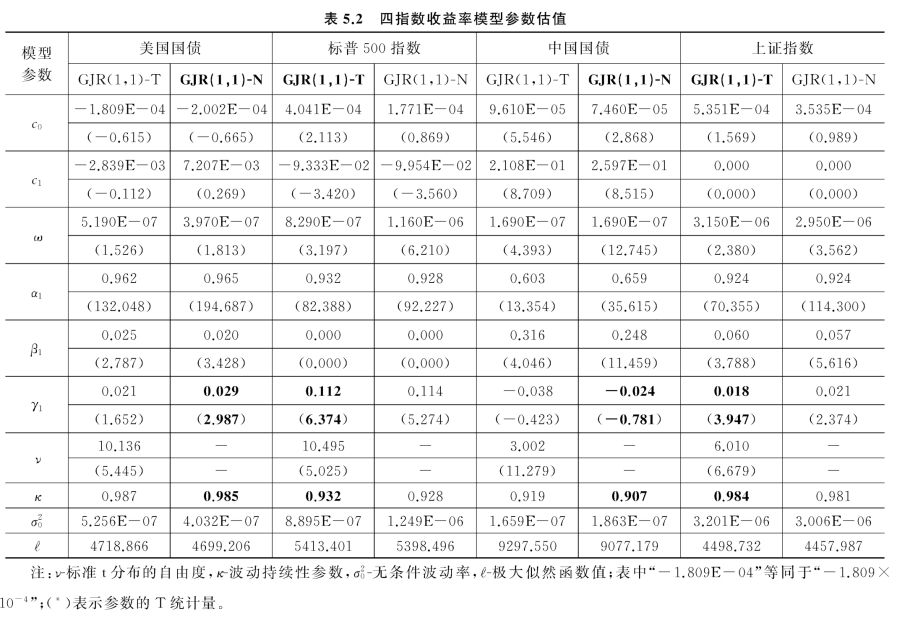
表5.1显示：K-S统计量表明在1%显著水平下股指收益率显著异于正态分布，峰度都大于3，具有明显的“尖峰厚尾”现象；ADF 统计量表明在5%显著水平下四个序列平稳且无单位根；滞后1至5阶的自相关系数是否联合为0的Q(5)统计量表明在5%显著水平四个收益率序列存在自相关现象，Q2(5)表明四个收益率平方序列均具有自相关现象，说明收益率序列波动聚类现象十分显著。因此边缘模型设定为还能刻画市场的非对称等特征的AR(1)-GJR-GARCH(1，1)模型：

其中s t－1＝1，εt－1＜0，s t－1＝0，εt－1≥0，系数还满足GARCH 约束条件，g(.)设定为正态分布(N)、学生t分布(T)，模型拟合结果见表5.2。

由表5.2可知：GJR-GARCH(1，1)-T 模型的极大似然函数值比GJRGARCH(1，1)-N 模型的大，前者的波动持续性参数κ 也大于后者，非对称参数γ1 小于后者。因此，描述四个指数收益率结构的模型分别设定为：AR(1)-GJR-GARCH(1，1)-N；AR(1)-GJR-GARCH(1，0)-T；AR(1)-GJR-GARCH(1，1)-N；AR(1)-GJR-GARCH(1，1)-T。参数估值表明：新息对美国债市与股市有同质的非对称性冲击特征，波动对前者的持续性强于后者；新息对中国债市与股市有异质的非对称性冲击特征，波动对前者的持续性弱于后者；新息对美国债市与中国债市有同质的非对称性冲击特征，波动对前者的持续性强于后者；新息对美国股市与中国股市有同质的非对称性冲击特征，波动对前者的持续性弱于后者。对此我们结合当前世界宏观经济金融调控的政策实情，进而可见：第一，中美两国的经济发展水平及其自身的市场开放程度决定了股市与债市的个性差异及市场的成熟度；第二，美元作为世界储备货币决定了美国股市与债市之间特有的波动特征；第三，中国作为最大的经济发展体，中国的资本市场还不够成熟，有许多值得完善的市场体制和金融制度需要政府大刀阔斧地推进，比如人民币的国际化与区域贸易结算的世界功能定位等，用以逐步消除其股市与债市之间的“跷跷板现象”。

表5.3　基于小波收缩估计量的均方积分误差

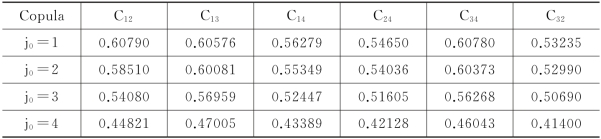
注：Cij-表示指数收益率i、j之间的Copula 函数，其中i，j∈{TNX，SP500，ZGGZ，SSEC}。

在对以上四个边缘模型分析中，我们并没考虑到新息对市场潜在相依结构的彼此影响，下面运用第二节介绍的Copula线性小波估计量与优化算法，识别四个序列所拟合模型的标准化残差序列之间的局部相依结构，同时筛选出最佳的参数Copula模型用以度量两两之间的潜在相依结构。我们利用Wav Lab8.5工具箱(也可用R 软件)编写程序：执行算法步骤1～5，实现对样本相依结构的小波线性估计，执行算法步骤6～7，实现最优化筛选参数Copula模型，结果见表5.3～5.5和图5.1。

表5.3给出了不同分解尺度上小波线性估计量的均方积分误差。其中数据表明随着尺度j0增加，小波线性估计量对美国国债、标普500指数、中国国债、上证综合指数等两两之间组合所得的六个Copula的估值均方积分误差越来越小。由此选取尺度j0＝4的小波线性估计量作为以上6个潜在相依结构的最佳估计量，详见图5.1的子图(1)～(6).(www.xing528.com)

表5.4　基于小波收缩估计量的Copula参数优化的最小均方积分误差

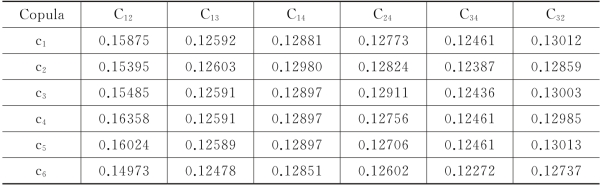
注：Cij-表示指数收益率i、j之间的Copula 函数，其中i，j∈{TNX，SP500，ZGGZ，SSEC}；Ci-表示常见参数Copula，i∈{N、T、G、C、F}以及混合Copula(C6)。

表5.4给出了基于小波最佳估计量的参数Copula筛选结果的均方积分误差(由式(5.14)给出)，其中c1～c6依次为高斯正态N-Copula族、学生TCopula族、冈贝G-Copula族、凯莱C-Copula族、富兰克F-Copula族和这五个族构成的混合Copula族。纵向比较均方积分误差的值，我们发现单一参数Copula的估值误差都比混合Copula的大，表明混合Copula族是所有参数Copula族中最好的Copula模型，用以刻画标准化残差之间潜在的相依结构特征，这也证明混合Copula族整合了所有单一参数Copula族的共同优点，从而实现对样本潜在相依结构的最佳建模。

表5.5给出了基于小波最佳估计量的参数Copula筛选结果与参数最优化估值。我们发现：单一参数Copula族的最优化估值与其在混合参数Copula族的估值有明显的差异，这在于后者在包容前者的不足之时，综合了其共同优势。混合参数Copula族中对应单一参数Copula的权重度量了其中单一参数Copula对样本相依结构描述的最大贡献力度。权重的正负体现了混合参数Copula族内单一参数Copula之间的和谐性，这使得多个单一参数Copula能共同增强相依结构的建模精度。

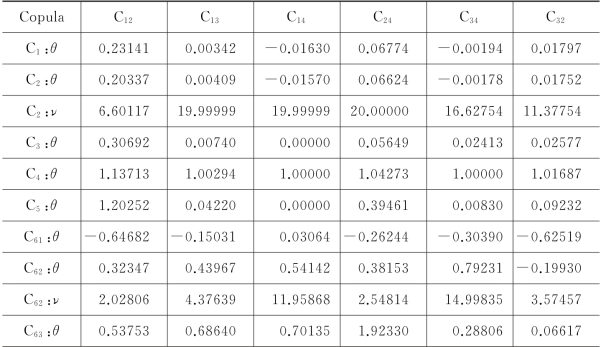
表5.5　基于小波的Copula参数优化

续表

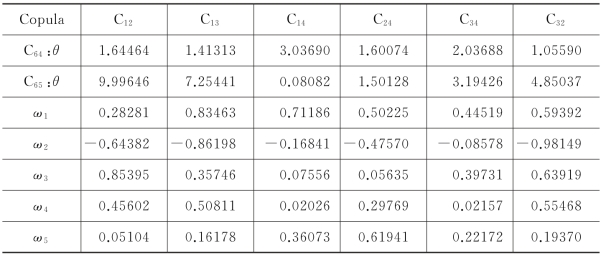
注：Cij-表示指数收益率i、j之间的Copula函数，其中i，j∈{TNX，SP500，ZGGZ，SSEC}；Ci-表示常见参数Copula，i∈{N、T、G、C、F}，wi-表示混合Copula(C6)中Ci的权重。

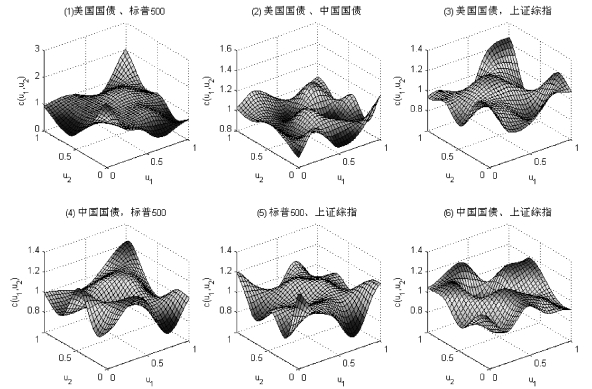
图5.1　指数收益率相依结构的小波线性估计量

图5.1(1)表明美国国债与标准普尔500指数之间的尾部相依特征十分明显，上尾特征比下尾特征突出，说明两个市场的协同性较强，同涨跌的可能性较大；图5.1(2)表明美国国债与中国国债之间的局部对角相依特征显著，进一步说明两个市场存在局部协同运动的趋势特征，也即可能存在局部时段的同涨跌现象，此外还存在局部异质性相依结构特征。图5.1(3)表明美国国债与上证综合指数之间的上尾相依特征比下尾相依特征明显，说明两个市场同涨的可能性较大，也存在局部的对角相依结构特征；图5.1(4)表明中国国债与标普500指数之间的上尾特征强于下尾特征，说明两个市场同涨的可能性较大，也存在局部的对冲相依结构特征；图5.1(5)表明标普500指数与上证指数之间的存在微弱的下尾相依结构特征，说明两个市场存在同跌的可能性，但局部的对冲相依结构特征明显；图5.1(6)表明中国国债与上证指数之间的存在较强的对冲相依结构特征，说明两个市场存在明显的局部异质相依结构特征，也即针对两个市场构建的组合投资可以使得风险被规避到最小值。