小波线性估计在金融风险价值量化分析中的应用

假设(X，Y)是二维实值随机向量，边缘分布函数分别为F(x)＝Pr(X＜x)和G(y)＝Pr(Y＜y)。根据Sklar(1959)[10]定理，则(X，Y)的联合分布为

其中C 为联合分布函数，边缘分布(U，V)＝(F(x)，G(y))∈(0，1)2 为均匀分布。事实上，一般未知H 的解析式，在F，G 和C属于确定的分布函数簇的条件下，利用MLE等经典的统计推断方法建立三者之间的解析式关系。因此，从C的解析式明确了(X，Y)之间的相依结构，改变X，Y 的边缘分布不会影响C的函数形式。然而在未知F，G 和C所属的分布函数簇时，常常利用边缘分布的经验分布对潜在Copula进行统计推断。假设(X 1，Y 1)，…，(X T，Y T)是从未知分布H 中抽取的T 组样本，(R i，S i)表示(X i，Y i)秩序统计量，经验分布函数为[F T(X i)，G T(Y i)]＝(R i/T，S i/T)，i∈{1，…，T}。易见，(R i/T，S i/T)表示从C(u，v)中随机抽取的不可观测边缘分布(U i，V i)的样本值，容易证明c(u，v)∈L 2(R 2)。由于样本的经验分布是其无偏估计量，因此将其代替真实的边缘分布，对(X，Y)的Copula密度c(u，v)进行统计推断。再利用式(5.3)、(5.6)和(5.7)，可得：

其中系数分别为

注意c(u，v)是二元概率密度函数，因此αj 0，k和β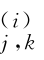的样本矩估计为(www.xing528.com)

在适当尺度J max≥j 0≥1，对式(5.9)截断得到c(u，v)的线性估计量为

由于Copula密度的尺度截断量c j 0在正方形[0，1]2 的某些区域内可能取负值，使得其积分和小于1。因此，线性估计量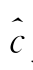j 0 未必是一个标准的Copula密度，但可以规范化为一个Copula密度。线性估计量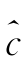j 0 明确地将潜在Copula密度分解为趋势估计量和水平、垂直、对角等三个方向上的细节估计量，基于分解尺度的变化，该估计量逐步识别出真实Copula的主体趋势和局部细节的动态演进特征。