VaR模型压力测试及准确性检验方法

VaR模型的压力测试就是要检验估计VaR 时所给定的置信水平与实际已发生及将要发生的情况是否吻合，当损失超过VaR 的天数过多时，说明VaR 模型低估了实际的风险水平；当损失超过VaR 的天数过少时，说明VaR模型过于保守而高估了实际的风险水平。VaR 模型的准确性检验方法主要包括失败检验法、分布预测法、超额损失大小检验法、方差检验法、概率预测法以及风险轨迹检验法等。Kupiec(1995)提出了一种常用的检验方法，他把收益率超过VaR 的例外情形看作从一个二项分布中出现的独立事件，假设估计VaR 的置信度为1－ϑ，样本容量为T，失效天数为F，则失效率为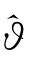＝F/T，失效率的期望值为ϑ。基于此法，本节对 的估计结果见表4.5。

表4.5　基于GJR-GARCH(1，1)模型的动态VaR 失败率估计结果

注4.3：^ϑN 表示z t 服从N(0，1)；^ϑW 表示z t 服从密度函数为~p(z)的分布。

表4.5给出了VaR 失败率的小波估计W 和正态分布估计N。BS准则密度估计误差明显要比标准正态分布的估计误差小，表明多尺度模型对四个市场的动态风险aR t()的估值效果得到了明显的改进。利用Kupiec(1995)提出的似然比率LR 检验统计量检验原假设ϑ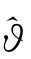＝ 是否成立，使得对VaR 估值准确性的评估就转化为检验失效率 是否显著等于ϑ，其中LR＝－2ln[(1－ϑ)T－FϑF]＋2ln[(1－)T－FF]。在原假设下LR 服从χ2(1)分布，如果LR＜临界值，则接受原假设，即VaR 明显得到改进。

表4.6、表4.7给出样本内动态aR t()的估值描述及检验结果，其中1%，5%，10%显著水平χ2(1)临界值分别为6.6348，3.8414，2.7055。

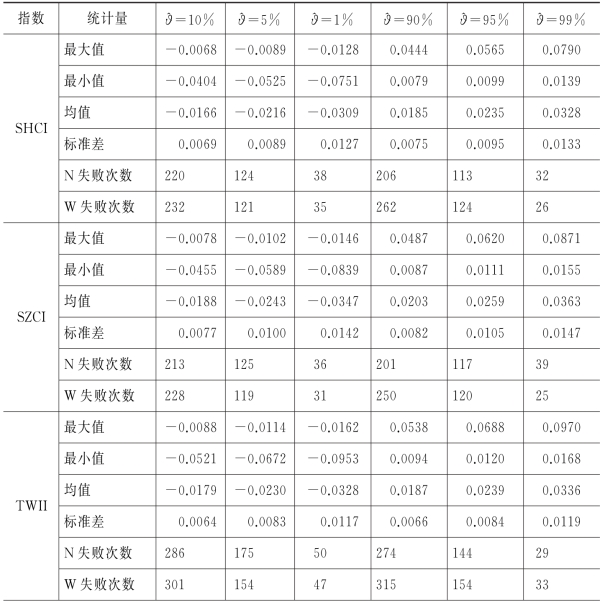
表4.6　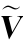aR t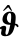)统计描述及失败次数

(www.xing528.com)

续表

注：%1.4N 表示基于N(0，1)分布；W 表示基于~p(z)校正的N(^μ，^σ2)分布。

表4.7　aR t()的动态检验结果

注4.5：(*)表示10%显著；(**)表示5%显著；(***)表示1%显著；[-]表示不显著。

由表4.7可见：(1)比较统计量LR 的值，发现小波估计的比正态分布的明显小，这意味着W 比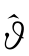N 的估计偏差小；(2)比较四个指数收益率动态VaR检验的显著性，则ϑ＝0.9，0.95，0.05对应的四个LR 值都是10%或5%显著。对于上证指数而言ϑ＝0.99N 的卡方检验结果不显著，BS小波估计W 的卡方检验结果1%显著。对台湾加权指数而言，两种估计方法的卡方检验结果都不显著，但是后者的LR 值比前者大。对香港恒生指数而言，两种估计方法的卡方检验结果都是1%显著，但LR 相差不大。对深证指数而言ϑ＝0.1，N 的卡方检验结果都不显著，相反BS小波估计的结果都显著。

总而言之，上述分析表明基于BS准则的aR t)明显提高了估计精度；四大股市指数收益率的左尾风险和右尾风险(分别对应了下跌风险和上涨风险，或者多头风险和空头风险)不具有对称性；由于本章充分利用了数据的局部特征，所以对尾部风险价值的估计明显优越于传统方法；动态VaR 的统计分析(见表4.6)也表明样本区间内四大股指的风险排序关系为TWII＞SHCI＞SZCI＞HSI。