金融风险价值量化分析：参数估计与校正

为了消除新息对大中华区内四大股指收益冲击的非对称性特征对分布密度局部特征的影响，根据表4.3的检验结果及已有文献的实证经验，我们首先对收益率序列建立GJR-GARCH(1，1)-N 模型，其次估计信息序列密度的小波估计量，接着通过最小化MSE校正正态密度的参数，最后分别计算VaR 的值。步骤如下

步骤1:拟合GJR-GARCH(1，1)-N 参数

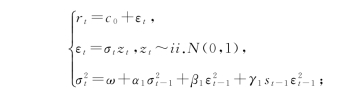
步骤2:按式(4.6)计算信息z t 的密度函数的小波阈值估计量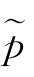(z)；

步骤3:以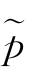(z)为基准，利用最优化方法对事先设定的p(z)＝N(0，1)标准正态密度进行参数校正，也即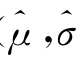)＝arg(μ，σ)∈R 2 min MSE(p，μ，σ)。其中MSE(p，μ，σ)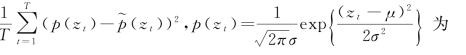＝正态密度；

步骤4:采用多尺度模型计算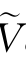aR(ϑ)，ϑ＝0.9，0.95，0.99。

再次利用Wav Lab8.5工具箱编写程序，执行上述算法的结果见表4.4和图4.3。我们发现基于BS规则的密度估计子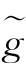(z)的实证效果也是最好的。

由表4.4可见：

1.模型的参数估值都是显著的，只有c 0 的t值小于2；α1＋β1 非常接近1，这表明四个市场明显存在波动持续性特征；(www.xing528.com)

2.比较γ1 值的大小，我们发现四个市场的非对称性强度依次为HSI＞TWI＞SHCI＞SZCI；

3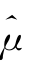 和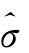 的值表明BS小波估计量校正Zt服从的N(0，1)分布的密度参数是合理的，这在于我们充分考虑到了样本数据的局部波动特征，而标准正态分布忽略了样本局部的奇异特征；

4.均方误差MSE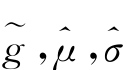)的偏序关系为SZCI＞SHCI＞TWI＞HSI，这说明先验假设的标准正态分布偏离基于BS 阈值规则的小波密度的大小关系，图4.3也暗示了这点是吻合逻辑的。

表4.4　模型参数估值及密度校正结果

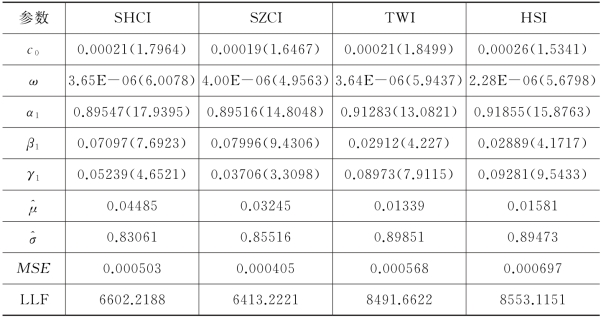
注4.2：(.)表示参数对应的t统计量值，^μ、^σ 分别是对正态分布的均值0和标准差1的校正值，MSE 为校正的最小准则值，LLF为模型的似然函数值。

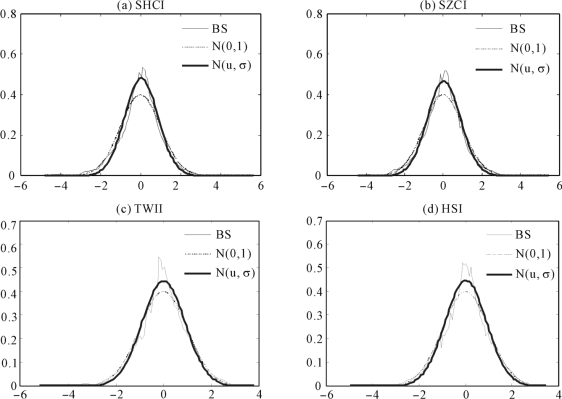
图4.3　新息分布参数校正结果

总而言之，以上对密度参数的校正目的就是要发现潜在真实的分布密度函数，以此实现对先验正态分布的改进。下面从VaR(ϑ)的压力测试的角度，检验风险价值的多尺度估值模型的可行性和合理性。